
已知函數
(1)求 的值域;
的值域;
(2)設 ,函數
,函數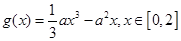 .若對任意
.若對任意 ,總存在
,總存在 ,使
,使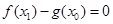 ,求實數
,求實數 的取值范圍.
的取值范圍.
(1) 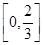 ;(2)
;(2)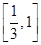
解析試題分析:(1)求出
科目:高中數學
來源:
題型:解答題
某商場銷售某種商品的經驗表明,該商品每日的銷售量
科目:高中數學
來源:
題型:解答題
已知函數
科目:高中數學
來源:
題型:解答題
已知函數
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區 的導函數,令導函數等于求出
的導函數,令導函數等于求出 的值,然后由
的值,然后由 的值,分區間討論導函數的正負得到函數的單調區間,根據函數的增減性得到函數的最大值和最小值即可得到
的值,分區間討論導函數的正負得到函數的單調區間,根據函數的增減性得到函數的最大值和最小值即可得到 的值域;(2)設函數
的值域;(2)設函數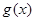 在[0,2]上的值域是A,根據題意對任意
在[0,2]上的值域是A,根據題意對任意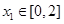 ,總存在
,總存在 ,使
,使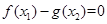 ,得到區間
,得到區間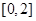 是A的子集,求出
是A的子集,求出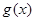 的導函數,分
的導函數,分 小于0和
小于0和 大于0兩種情況討論導函數的正負得到函數的單調區間,根據函數的增減性得到函數的最大值和最小值,即可得到函數在相應區間的值域,根據區間[0,2]是A的子集判斷出符合這一條件的情況,列出關于
大于0兩種情況討論導函數的正負得到函數的單調區間,根據函數的增減性得到函數的最大值和最小值,即可得到函數在相應區間的值域,根據區間[0,2]是A的子集判斷出符合這一條件的情況,列出關于 的不等式,求出不等式的解集即可得到滿足題意
的不等式,求出不等式的解集即可得到滿足題意 的取值范圍.
的取值范圍.
試題解析:(1)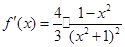 ,令
,令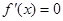 ,得
,得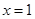 或
或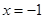 .
.
當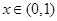 時,
時,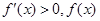 在
在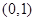 上單調遞增;
上單調遞增;
當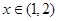 時,
時,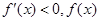 在
在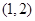 上單調遞減,
上單調遞減,
而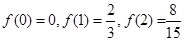 ,
, 當
當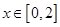 時,
時, 的值域是
的值域是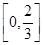 .
.
(2)設函數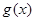 在
在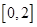 上的值域是A,
上的值域是A,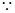 若對任意
若對任意 .總存在
.總存在 1,使
1,使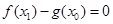 ,
,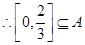 .
. 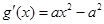 .
.
①當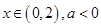 時,
時,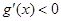 ,
,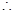 函數
函數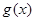 在
在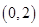 上單調遞減.
上單調遞減. 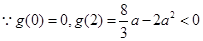 ,當
,當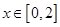 時,不滿足
時,不滿足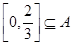 ;
;
②當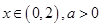 時,
時,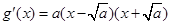 ,令
,令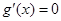 ,得
,得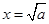 或
或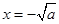 (舍去)
(舍去)
(i)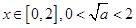 時,
時,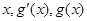 的變化如下表:
的變化如下表:
0 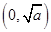
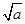
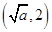
2 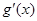


驕子之路寒假作業河北人民出版社系列答案
冬之卷快樂假日系列答案
動力源期末寒假作業系列答案
非常完美完美假期寒假作業系列答案
新浪書業復習總動員學期總復習寒系列答案

自主假期作業本吉林大學出版社系列答案
高中新課程寒假作業系列答案
海淀黃岡寒假作業合肥工業大學出版社系列答案
寒假Happy假日系列答案
 (單位:千克)與銷售價格
(單位:千克)與銷售價格 (單位:元/千克)滿足關系式
(單位:元/千克)滿足關系式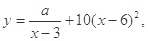 其中
其中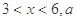 為常數.己知銷售價格為5元/千克時,每日可售出該商品11千克.
為常數.己知銷售價格為5元/千克時,每日可售出該商品11千克.
(1)求 的值;
的值;
(2)若該商品的成本為3元/千克,試確定銷售價格 的值,使商場每日銷售該商品所獲得利潤最大.
的值,使商場每日銷售該商品所獲得利潤最大.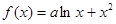 (
( 為實常數)
為實常數)
(1)當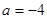 時,求函數
時,求函數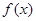 在
在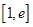 上的最大值及相應的
上的最大值及相應的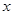 值;
值;
(2)當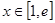 時,討論方程
時,討論方程 根的個數
根的個數
(3)若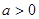 ,且對任意的
,且對任意的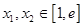 ,都有
,都有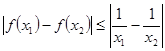 ,求實數a的取值范圍
,求實數a的取值范圍  ,設曲線
,設曲線 在與
在與 軸交點處的切線為
軸交點處的切線為 ,
, 為
為 的導函數,滿足
的導函數,滿足 .
.
(1)求 ;
;
(2)設 ,
, ,求函數
,求函數 在
在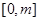 上的最大值;
上的最大值;
(3)設 ,若對于一切
,若對于一切 ,不等式
,不等式 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號