
(07年湖南卷理)(12分)
如圖2,![]() 分別是矩形
分別是矩形![]() 的邊
的邊![]() 的中點,
的中點,![]() 是
是![]() 上的一點,將
上的一點,將![]() ,
,![]() 分別沿
分別沿![]() 翻折成
翻折成![]() ,
,![]() ,并連結(jié)
,并連結(jié)![]() ,使得平面
,使得平面![]()
平面![]() ,
,![]() ,且
,且![]() .連結(jié)
.連結(jié)![]() ,如圖3.
,如圖3.
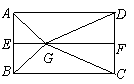
圖2
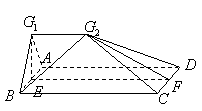
圖3
(I)證明:平面![]() 平面
平面![]() ;
;
(II)當(dāng)![]() ,
,![]() ,
,![]() 時,求直線
時,求直線![]() 和平面
和平面![]() 所成的角.
所成的角.
解析:解法一:(I)因為平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以平面![]()
![]() 平面
平面![]() .
.
(II)過點![]() 作
作![]() 于點
于點![]() ,連結(jié)
,連結(jié)![]() .
.
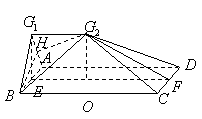
由(I)的結(jié)論可知,![]() 平面
平面![]() ,
,
所以![]() 是
是![]() 和平面
和平面![]() 所成的角.
所成的角.
因為平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]() ,
,![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,故
,故![]() .
.
因為![]() ,
,![]() ,所以可在
,所以可在![]() 上取一點
上取一點![]() ,使
,使![]() ,
,
又因為![]() ,所以四邊形
,所以四邊形![]() 是矩形.
是矩形.
由題設(shè)![]() ,
,![]() ,
,![]() ,則
,則![]() .所以
.所以![]() ,
,
![]() ,
,![]() ,
,![]() .
.
因為![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,從而
,從而![]() .
.
故![]() ,
,![]() .
.
又![]() ,由
,由![]() 得
得![]() .
.
故![]() .
.
即直線![]() 與平面
與平面![]() 所成的角是
所成的角是![]() .
.
解法二:(I)因為平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]() ,
,![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,從而
,從而![]() .又
.又![]() ,
,
所以![]() 平面
平面![]() .因為
.因為![]() 平面
平面![]() ,所以平面
,所以平面![]()
![]() 平面
平面![]() .
.
(II)由(I)可知,![]() 平面
平面![]() .故可以
.故可以![]() 為原點,分別以直線
為原點,分別以直線![]()
為![]() 軸、
軸、![]() 軸、
軸、![]() 軸建立空間直角坐標(biāo)系(如圖),
軸建立空間直角坐標(biāo)系(如圖),

由題設(shè)![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,
![]() ,
,![]() ,相關(guān)各點的坐標(biāo)分別是
,相關(guān)各點的坐標(biāo)分別是![]() ,
,
![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
設(shè)![]() 是平面
是平面![]() 的一個法向量,
的一個法向量,
由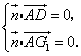 得
得![]() 故可取
故可取![]() .
.
過點![]() 作
作![]() 平面
平面![]() 于點
于點![]() ,因為
,因為![]() ,所以
,所以![]() ,
,
于是點![]() 在
在![]() 軸上.
軸上.
因為![]() ,所以
,所以![]() ,
,![]() .
.
設(shè)![]() (
(![]() ),由
),由![]() ,解得
,解得![]() ,
,
所以![]() .
.
設(shè)![]() 和平面
和平面![]() 所成的角是
所成的角是![]() ,則
,則
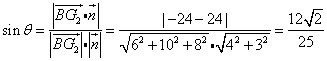 .
.
故直線![]() 與平面
與平面![]() 所成的角是
所成的角是![]() .
.


 暑假作業(yè)暑假快樂練西安出版社系列答案
暑假作業(yè)暑假快樂練西安出版社系列答案 新活力總動員暑系列答案
新活力總動員暑系列答案科目:高中數(shù)學(xué) 來源: 題型:
(07年湖南卷理)將楊輝三角中的奇數(shù)換成1,偶數(shù)換成0,得到如圖1所示的0-1三角數(shù)表.從上
往下數(shù),第1次全行的數(shù)都為1的是第1行,第2次全行的數(shù)都為1的是第3行,…,第![]() 次全行的數(shù)都為1的是第 行;第61行中1的個數(shù)是 .
次全行的數(shù)都為1的是第 行;第61行中1的個數(shù)是 .
第1行 1 1
第2行 1 0 1
第3行 1 1 1 1
第4行 1 0 0 0 1
第5行 1 1 0 0 1 1
…… ………………………………
圖1
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(07年湖南卷理)(12分)
如圖2,![]() 分別是矩形
分別是矩形![]() 的邊
的邊![]() 的中點,
的中點,![]() 是
是![]() 上的一點,將
上的一點,將![]() ,
,![]() 分別沿
分別沿![]() 翻折成
翻折成![]() ,
,![]() ,并連結(jié)
,并連結(jié)![]() ,使得平面
,使得平面![]()
平面![]() ,
,![]() ,且
,且![]() .連結(jié)
.連結(jié)![]() ,如圖3.
,如圖3.
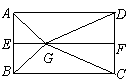
圖2

圖3
(I)證明:平面![]() 平面
平面![]() ;
;
(II)當(dāng)![]() ,
,![]() ,
,![]() 時,求直線
時,求直線![]() 和平面
和平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(07年湖南卷理)(12分)
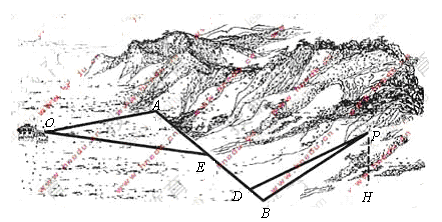
如圖4,某地為了開發(fā)旅游資源,欲修建一條連接風(fēng)景點![]() 和居民區(qū)
和居民區(qū)![]() 的公路,點
的公路,點![]() 所在的山坡面與山腳所在水平面
所在的山坡面與山腳所在水平面![]() 所成的二面角為
所成的二面角為![]() (
(![]() ),且
),且![]() ,點
,點![]() 到平面
到平面![]() 的距離
的距離![]() (km).沿山腳原有一段筆直的公路
(km).沿山腳原有一段筆直的公路![]() 可供利用.從點
可供利用.從點![]() 到山腳修路的造價為
到山腳修路的造價為![]() 萬元/km,原有公路改建費用為
萬元/km,原有公路改建費用為![]() 萬元/km.當(dāng)山坡上公路長度為
萬元/km.當(dāng)山坡上公路長度為![]() km(
km(![]() )時,其造價為
)時,其造價為![]() 萬元.已知
萬元.已知![]() ,
,![]() ,
,![]() ,
,![]() .
.
(I)在![]() 上求一點
上求一點![]() ,使沿折線
,使沿折線![]() 修建公路的總造價最小;
修建公路的總造價最小;
(II) 對于(I)中得到的點![]() ,在
,在![]() 上求一點
上求一點![]() ,使沿折線
,使沿折線![]()
修建公路的總造價最小.
(III)在![]() 上是否存在兩個不同的點
上是否存在兩個不同的點![]() ,
,![]() ,使沿折線
,使沿折線![]() 修建公路的
修建公路的
總造價小于(II)中得到的最小總造價,證明你的結(jié)論.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com