
在 中,滿足
中,滿足 ,
, 是
是 邊上的一點.
邊上的一點.
(Ⅰ)若 ,求向量
,求向量 與向量
與向量 夾角的正弦值;
夾角的正弦值;
(Ⅱ)若 ,
, =m
(m為正常數) 且
=m
(m為正常數) 且 是
是 邊上的三等分點.,求
邊上的三等分點.,求 值;
值;
(Ⅲ)若 且
且 求
求 的最小值。
的最小值。
(Ⅰ)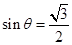 ;
;
(Ⅱ)(1)當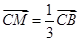 時,則
時,則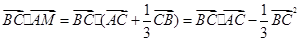 =
=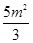 ;
;
(2)當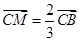 時,則
時,則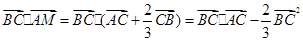 =
=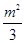 ;
;
(Ⅲ)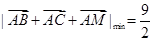 .
.
【解析】
(Ⅰ)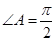 ,
,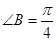 可得
可得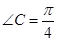 ,
,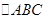 是等腰直角三角形,令
是等腰直角三角形,令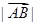 =
=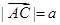 ;
;
(Ⅱ)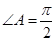 ,
,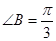 ,
,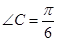 ,
,
利用30°的直角三角形的性質令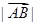 =m所以
=m所以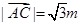 ,
,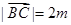 ,
,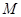 是
是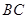 邊上的三等分點.分類討論:
邊上的三等分點.分類討論: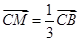 或
或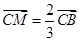 ;
;
(Ⅲ)注意到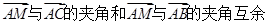 ,是解題的關鍵,
,是解題的關鍵,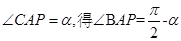 ,求
,求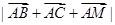 通常用平方的方法。
通常用平方的方法。
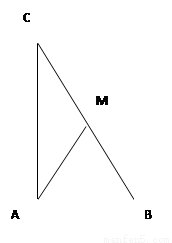
(Ⅰ)解:設向量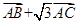 與向量
與向量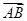 的夾角為
的夾角為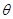 ,則
,則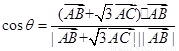
令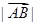 =
=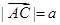 ,得
,得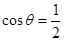 ,又
,又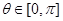 ,則
,則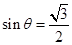 為所求……………2分
為所求……………2分
(Ⅱ)解:因為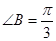 ,
,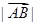 =m所以
=m所以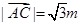 ,
,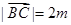
(1)當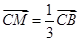 時,則
時,則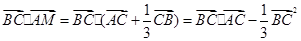 =
=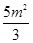 ;--2分
;--2分
(2)當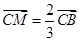 時,則
時,則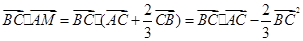 =
=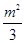 ;---2分
;---2分
(Ⅲ)解:設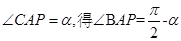 ,因為
,因為
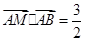 ,
,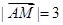 ;
;
所以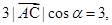 即
即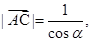 于是
于是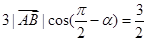 得
得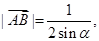
從而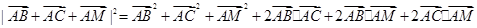 ---2分
---2分
=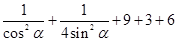 =
=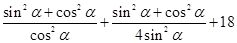
=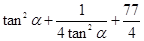 …………………………………2分
…………………………………2分
令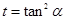 ,
,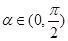 則
則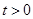 ,則函數
,則函數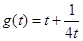 ,在
,在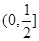 遞減,在
遞減,在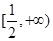 上遞增,所以
上遞增,所以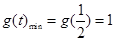 從而當
從而當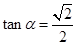 時,
時,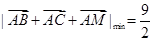 ………………2分
………………2分


 南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案科目:高中數學 來源:2013-2014學年浙江省建人高復高三上學期第二次月考理科數學試卷(解析版) 題型:解答題
在 中,滿足:
中,滿足: ,
, 是
是 的中點.
的中點.
(1)若 ,求向量
,求向量 與向量
與向量 的夾角的余弦值;
的夾角的余弦值;
(2)若點 是
是 邊上一點,
邊上一點, ,且
,且 ,求
,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源:2012學年浙江省杭州七校高一第二學期期中聯(lián)考數學試卷(解析版) 題型:解答題
在 中,滿足
中,滿足 ,
, 是
是 邊上的一點.
邊上的一點.
(Ⅰ)若 ,求向量
,求向量 與向量
與向量 夾角的正弦值;
夾角的正弦值;
(Ⅱ)若 ,
, =m (m為正常數) 且
=m (m為正常數) 且 是
是 邊上的三等分點.,求
邊上的三等分點.,求 值;
值;
(Ⅲ)若 且
且 求
求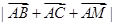 的最小值。
的最小值。
【解析】第一問中,利用向量的數量積設向量 與向量
與向量 的夾角為
的夾角為 ,則
,則
令 =
= ,得
,得 ,又
,又 ,則
,則 為所求
為所求
第二問因為 ,
, =m所以
=m所以 ,
,
(1)當 時,則
時,則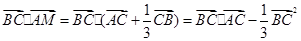 =
=
(2)當 時,則
時,則 =
=
第三問中,解:設 ,因為
,因為
 ,
, ;
;
所以 即
即 于是
于是 得
得
從而
運用三角函數求解。
(Ⅰ)解:設向量 與向量
與向量 的夾角為
的夾角為 ,則
,則
令 =
= ,得
,得 ,又
,又 ,則
,則 為所求……………2分
為所求……………2分
(Ⅱ)解:因為 ,
, =m所以
=m所以 ,
,
(1)當 時,則
時,則 =
= ;-2分
;-2分
(2)當 時,則
時,則 =
= ;--2分
;--2分
(Ⅲ)解:設 ,因為
,因為
 ,
, ;
;
所以 即
即 于是
于是 得
得
從而 ---2分
---2分
= =
=
= …………………………………2分
…………………………………2分
令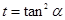 ,
, 則
則 ,則函數
,則函數 ,在
,在 遞減,在
遞減,在 上遞增,所以
上遞增,所以 從而當
從而當 時,
時,
查看答案和解析>>
科目:高中數學 來源:2013屆江蘇無錫市高二第二學期期中文科數學試卷(解析版) 題型:解答題
在 中,滿足
中,滿足 ,
, 是
是 中點.
中點.
(1)若 ,求向量
,求向量 與向量
與向量 的夾角的余弦值;
的夾角的余弦值;
(2)若 是線段
是線段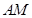 上任意一點,且
上任意一點,且 ,求
,求 的最小值;
的最小值;
(3)若點 是
是 邊上一點,且
邊上一點,且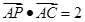 ,
,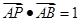 ,
, ,求
,求 的最小值.
的最小值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com