
已知函數
(1)求函數 的單調區間.
的單調區間.
(2)若方程 有4個不同的實根,求
有4個不同的實根,求 的范圍?
的范圍?
(3)是否存在正數 ,使得關于
,使得關于 的方程
的方程 有兩個不相等的實根?如果存在,求b
有兩個不相等的實根?如果存在,求b 滿足的條件,如果不存在,說明理由.
滿足的條件,如果不存在,說明理由.
(1)增區間為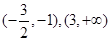 ,減區間為
,減區間為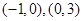 ;(2)
;(2) ;(3)不存在,理由見詳解.
;(3)不存在,理由見詳解.
解析試題分析:(1)首先求導函數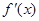 ,然后通過判斷
,然后通過判斷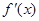 的符號可求得單調區間;(2)構造函數
的符號可求得單調區間;(2)構造函數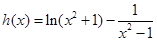 ,然后利用導數研究函數的取值變化,確定圖象的位置,由圖象可直觀得到函
,然后利用導數研究函數的取值變化,確定圖象的位置,由圖象可直觀得到函 的取值范圍;(3)
的取值范圍;(3)
試題解析:(1)根據 定義域后,求導得到
定義域后,求導得到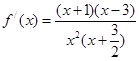 ,
,
根據導數和0的關系得到在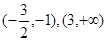 是函數
是函數 的增區間;在
的增區間;在 是函數
是函數 減區間.
減區間.
(2)(2)令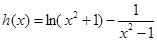 ,求導得
,求導得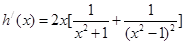 ,
,
里面有一個零點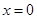 和兩個斷點
和兩個斷點 ,所以初步可以得到函數在區間
,所以初步可以得到函數在區間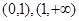 單調增;在區間
單調增;在區間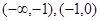 單調減.
單調減.
當 從負半軸方向趨近于-1時,
從負半軸方向趨近于-1時,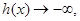
當 從正半軸方向趨近于-1時,
從正半軸方向趨近于-1時,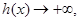
而且 時,
時,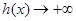 ,
,
而且可以很容易得到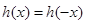 ,函數為偶函數,而且
,函數為偶函數,而且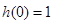 ,
,
另半邊的圖像就容易模擬得到了,所以 有4個不同的實根,結合圖像得到
有4個不同的實根,結合圖像得到 .
.
(本題必須另半邊如果不分析必須用奇偶性說明;而且必須說明在斷點處的趨勢,否則扣2到3分)
(3)結論:這樣的正數 不存在.
不存在.
假設存在滿足條件的 ,使得方程
,使得方程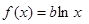 存在兩個不相等的實根
存在兩個不相等的實根 和
和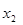 ,然后代入方程,根據其結構利用第(1)問的結論判斷出
,然后代入方程,根據其結構利用第(1)問的結論判斷出 在
在 上的取值及單調性,然后結合假設導出矛盾,作出判斷.
上的取值及單調性,然后結合假設導出矛盾,作出判斷.
假設存在正數 ,使得方程
,使得方程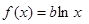 存在兩個不相等的實根
存在兩個不相等的實根 和
和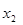 ,則
,則
根據定義域知道 和
和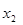 都是正數.
都是正數.
根據第1問知道,當 時,函數的最小值
時,函數的最小值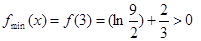 ,
,
所以 ,
,
因為 ,等式兩邊同號,所以,
,等式兩邊同號,所以,
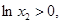 所以
所以

不妨設
由(1)(2)可得 ,
,
所以 ,
,
所以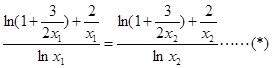 .
.
因為很容易證明到函數 在
在 為恒大于0且為減函數
為恒大于0且為減函數
所以(*)方程顯然不成立,因為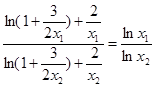 左邊大于1,右邊小于1.
左邊大于1,右邊小于1.
所以原假設:存在正數 ,使得方程
,使得方程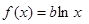 存在兩個不相等的實根
存在兩個不相等的實根 和
和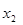 錯誤(本題其他證法,請酌情給分)
錯誤(本題其他證法,請酌情給分)
考點:1、導數與函數的單調性關系;2、探索性問題;3、函數與方程根的關系.


科目:高中數學 來源: 題型:解答題
某地方政府準備在一塊面積足夠大的荒地上建一如圖所示的一個矩形綜合性休閑廣場,其總面積為3000平方米,其中場地四周(陰影部分)為通道,通道寬度均為2米,中間的三個矩形區域將鋪設塑膠地面作為運動場地(其中兩個小場地形狀相同),塑膠運動場地占地面積為S平方米.
(1)分別寫出用x表示y和S的函數關系式(寫出函數定義域);
(2)怎樣設計能使S取得最大值,最大值為多少?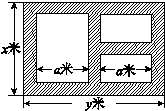
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
二次函數f(x)滿足f(x+1)-f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)在區間[-1,1]上,y=f(x)的圖象恒在y=2x+m的圖象上方,求實數m的取值范圍
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某通訊公司需要在三角形地帶 區域內建造甲、乙兩種通信信號加強中轉站,甲中轉站建在區域
區域內建造甲、乙兩種通信信號加強中轉站,甲中轉站建在區域 內,乙中轉站建在區域
內,乙中轉站建在區域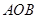 內.分界線
內.分界線 固定,且
固定,且 =
= 百米,邊界線
百米,邊界線 始終過點
始終過點 ,邊界線
,邊界線 滿足
滿足 .
.
設 (
( )百米,
)百米,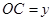 百米.
百米.
(1)試將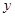 表示成
表示成 的函數,并求出函數
的函數,并求出函數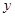 的解析式;
的解析式;
(2)當 取何值時?整個中轉站的占地面積
取何值時?整個中轉站的占地面積 最小,并求出其面積的最小值.
最小,并求出其面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
定義在 上的函數
上的函數 ,如果滿足:對任意
,如果滿足:對任意 ,存在常數
,存在常數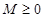 ,都有
,都有 成立,則稱
成立,則稱 是
是 上的有界函數,其中
上的有界函數,其中 稱為函數
稱為函數 的一個上界.已知函數
的一個上界.已知函數 ,
, .
.
(1)若函數 為奇函數,求實數
為奇函數,求實數 的值;
的值;
(2)在(1)的條件下,求函數 在區間
在區間 上的所有上界構成的集合;
上的所有上界構成的集合;
(3)若函數 在
在 上是以3為上界的有界函數,求實數
上是以3為上界的有界函數,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知定義在R上的奇函數f(x)滿足f(x-4)=-f(x).
(1)求f(2 012)的值;
(2)求證:函數f(x)的圖像關于直線x=2對稱;
(3)若f(x)在區間[0,2]上是增函數,試比較f(-25),f(11),f(80)的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com