
��֪�E�A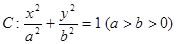 �^(gu��)�c(di��n)
�^(gu��)�c(di��n)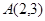 �����x����
�����x����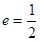 ��
��
��1����E�A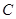 �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2���Ƿ�����^(gu��)�c(di��n)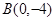 ��ֱ��
��ֱ��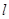 ���E�A�ڲ�ͬ�ă��c(di��n)M��N���ҝM��
���E�A�ڲ�ͬ�ă��c(di��n)M��N���ҝM��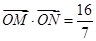 �������c(di��n)O������(bi��o)ԭ�c(di��n)���������ڣ����ֱ��
�������c(di��n)O������(bi��o)ԭ�c(di��n)���������ڣ����ֱ��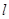 �ķ��̣��������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
�ķ��̣��������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
��1��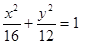 ��2������ֱ��
��2������ֱ��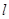 ��
��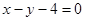 ��
��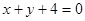 �M���}��
�M���}��
����ԇ�}��������1���ߙE�A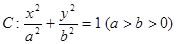 �^(gu��)�c(di��n)
�^(gu��)�c(di��n)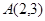 �����x����
�����x����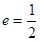 ��
��
��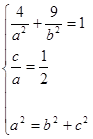 �� ����2��
�� ����2��
��ã�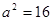 ,
,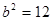 �� ����4��
�� ����4��
���E�A�ķ��̞飺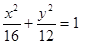 . ����5��
. ����5��
��2�����O(sh��)�����^(gu��)�c(di��n)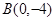 ��ֱ��
��ֱ��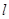 ���E�A�ڲ�ͬ�ă��c(di��n)M��N���ҝM��
���E�A�ڲ�ͬ�ă��c(di��n)M��N���ҝM��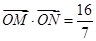 �� ����6��
�� ����6��
��ֱ��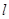 ��б�ʲ����ڣ���ֱ���^(gu��)�c(di��n)
��б�ʲ����ڣ���ֱ���^(gu��)�c(di��n)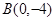 ���tֱ��
���tֱ��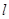 ����y�S����ֱ��,
����y�S����ֱ��,
��ֱ��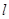 �c�E�A�ăɲ�ͬ���c(di��n)M��N���ǙE�A���S�Ķ��c(di��n),
�c�E�A�ăɲ�ͬ���c(di��n)M��N���ǙE�A���S�Ķ��c(di��n),
��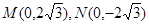 ,
,
��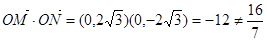 ,
,
��ֱ��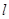 ��б�ʱش��ڣ������O(sh��)��k , ����7��
��б�ʱش��ڣ������O(sh��)��k , ����7��
����O(sh��)ֱ��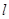 �ķ��̞飺
�ķ��̞飺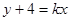 ����
���� ,
,
(li��n)��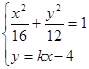 ,��y��
,��y�� 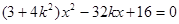 ,
,
��ֱ���c�E�A�ཻ�ڲ�ͬ�ă��c(di��n)M��N,
��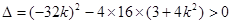 �ã�
�ã� �� ����8��
�� ����8��
�O(sh��)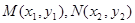 ,
,
��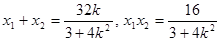 ,
,
��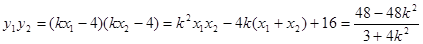 , ����9��
, ����9��
��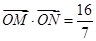 ,
,
��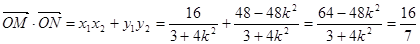 ,
,
����(ji��n)��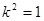 ,
,
��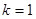 ��
��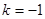 ����(j��ng)�z�(y��n)���M���ʽ, ����10��
����(j��ng)�z�(y��n)���M���ʽ, ����10��
��ֱ��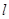 �ķ��̞飺
�ķ��̞飺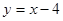 ��
��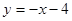 , ����11��
, ����11��
�����ֱ��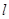 ��
��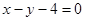 ��
��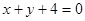 �M���}�⣮ ����12��
�M���}�⣮ ����12��
���c(di��n)����С�}��Ҫ����E�A�ķ��̼�ֱ���c�E�A��λ���P(gu��n)ϵ.
�c(di��n)�u(p��ng)���漰��ֱ���c�A�F������λ���P(gu��n)ϵ�r(sh��)�������Ҫ�O(sh��)��ֱ�����̣���Ҫ��ӛ���]ֱ����б���Ƿ���ڣ�(li��n)��ֱ���c�A�F�������̺�Ҫ��ӛ�(y��n)�C�Єeʽ������.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�O(sh��)�E�AC��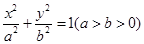 �����c(di��n)��F���^(gu��)�c(di��n)F��ֱ���c�E�AC�ཻ��A��B���c(di��n)��ֱ��l�ăAб�Ǟ�60o,
�����c(di��n)��F���^(gu��)�c(di��n)F��ֱ���c�E�AC�ཻ��A��B���c(di��n)��ֱ��l�ăAб�Ǟ�60o,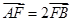 .
.
��E�AC���x���ʣ�
���|AB|=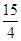 ����E�AC�ķ���.
����E�AC�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
����С�}�M��12�֣�
��D�E�A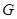 ��
��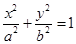
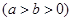 �ăɂ�(g��)���c(di��n)��
�ăɂ�(g��)���c(di��n)��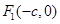 ��
�� ����c(di��n)
����c(di��n) ��
��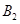 ��(g��u)����e��32��������.
��(g��u)����e��32��������.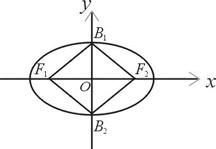
��1����˕r(sh��)�E�A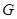 �ķ��̣�
�ķ��̣�
��2���O(sh��)б�ʞ�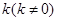 ��ֱ��
��ֱ�� �c�E�A
�c�E�A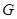 �ཻ�ڲ�ͬ�ă��c(di��n)
�ཻ�ڲ�ͬ�ă��c(di��n)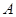 ��
��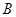 ��
��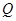 ��
��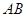 �����c(di��n)����
�����c(di��n)����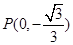 . ��(w��n)��
. ��(w��n)��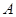 ��
��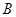 ���c(di��n)�ܷ��P(gu��n)��ֱ��
���c(di��n)�ܷ��P(gu��n)��ֱ��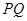 ��(du��)�Q. ���ܣ����
��(du��)�Q. ���ܣ���� ��ȡֵ�����������ܣ�Ո(q��ng)�f(shu��)������.
��ȡֵ�����������ܣ�Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
����С�}�M��12�֣�
��֪�E�AC������ԭ�c(di��n)�����c(di��n)��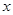 �S�ϣ�һ�l��(j��ng)�^(gu��)�c(di��n)
�S�ϣ�һ�l��(j��ng)�^(gu��)�c(di��n) �҃Aб������ֵ��
�҃Aб������ֵ��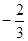 ��ֱ��
��ֱ��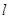 ���E�A��A��B���c(di��n)����
���E�A��A��B���c(di��n)����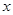 �S��M�c(di��n)����
�S��M�c(di��n)����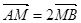 .
.
��1����ֱ��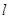 �ķ��̣�
�ķ��̣�
��2����E�AC�L(zh��ng)�S��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
����С�}�M��12�֣� ��ֱ֪��L��y=x+1�c����C�� ���ڲ�ͬ�ă��c(di��n)A,B;O������(bi��o)ԭ�c(di��n)��
���ڲ�ͬ�ă��c(di��n)A,B;O������(bi��o)ԭ�c(di��n)��
��1���� ��ԇ̽��������C�σH���ڎׂ�(g��)�c(di��n)��ֱ��L�ľ��xǡ��
��ԇ̽��������C�σH���ڎׂ�(g��)�c(di��n)��ֱ��L�ľ��xǡ�� �����f(shu��)�����ɣ�
�����f(shu��)�����ɣ�
��2����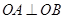 ����a>b,
����a>b, ,ԇ������C���x����e��ȡֵ������
,ԇ������C���x����e��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
����С�}�M��12�֣�
��֪�E�AC :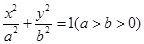 ��(j��ng)�^(gu��)�c(di��n)
��(j��ng)�^(gu��)�c(di��n)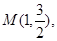 �x���ʞ�
�x���ʞ�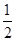 ��
��
���� ��E�AC�ķ��̣�
�����O(sh��)ֱ��l�c�E�AC�ཻ��A��B���c(di��n)���Ծ���OA��OB����߅��ƽ����߅��OAPB��������c(di��n)P�ڙE�AC�ϣ�O������(bi��o)ԭ�c(di��n)����O��ֱ��l�ľ��x����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
����С�}�M��13�֣���֪����������(bi��o)ԭ�c(di��n)O�����c(di��n)��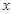 �S�ϣ��L(zh��ng)�S�L(zh��ng)�Ƕ��S�L(zh��ng)��2���ęE�A��(j��ng)�^(gu��)�c(di��n)M(2,1)
�S�ϣ��L(zh��ng)�S�L(zh��ng)�Ƕ��S�L(zh��ng)��2���ęE�A��(j��ng)�^(gu��)�c(di��n)M(2,1)
������E�A�ķ��̣�
����ֱ�� ƽ����
ƽ���� �����c�E�A����A��B�ɂ�(g��)��ͬ�c(di��n).
�����c�E�A����A��B�ɂ�(g��)��ͬ�c(di��n).
�������� ���g�ǣ���ֱ��
���g�ǣ���ֱ�� ��
�� �S�ϵĽؾ�m��ȡֵ������
�S�ϵĽؾ�m��ȡֵ������
���������Cֱ��MA��MB�cx�S���ɵ������ο��ǵ���������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
(���}�M��13��)
��֪�E�A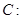
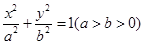 ���x���ʞ�
���x���ʞ�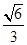 ���E�A���S�L(zh��ng)��
���E�A���S�L(zh��ng)��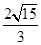 .
.
������E�A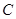 �ķ��̣�
�ķ��̣�
������֪?ji��ng)�ֱ��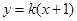 �c�E�A
�c�E�A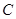 �ཻ��
�ཻ��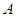 ��
��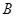 ���c(di��n). ��������
���c(di��n). ��������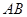 ���c(di��n)�ęM����(bi��o)��
���c(di��n)�ęM����(bi��o)��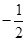 ����б��
����б��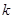 ��ֵ�������c(di��n)
��ֵ�������c(di��n)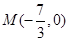 �����C��
�����C��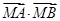 �鶨ֵ��
�鶨ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
(��С�}�M��12�֣�
��1����ֱ�� ���p����
���p���� �صõ����L(zh��ng)��
�صõ����L(zh��ng)��
��2�����^(gu��)���c(di��n) ��ֱ�����p����
��ֱ�����p���� �صõ������c(di��n)܉�E���̡�
�صõ������c(di��n)܉�E���̡�
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com