
(1)求點(diǎn)C的軌跡E的方程;
(2)是否存在直線l,使l過點(diǎn)(0,1)并與曲線E交于P、Q兩點(diǎn),且滿足![]() ·
·![]() =-2?若存在,求出直線l的方程;若不存在,說明理由.
=-2?若存在,求出直線l的方程;若不存在,說明理由.
解:(1)設(shè)C(x,y),其中xy≠0.由![]() =λ
=λ![]() (λ∈R且λ≠0),知MG∥AB.設(shè)G(a,b),則M(0,b),∴x=3a,y=3b①.
(λ∈R且λ≠0),知MG∥AB.設(shè)G(a,b),則M(0,b),∴x=3a,y=3b①.
∵M(jìn)是不等邊△ABC的外心,∴|MA|=|MC|,∴![]() =
=![]() ②,
②,
將①代入②化簡(jiǎn)整理得x2+![]() =1.所以點(diǎn)C的軌跡E的方程為x2+
=1.所以點(diǎn)C的軌跡E的方程為x2+![]() =1(xy≠0).
=1(xy≠0).
(2)假設(shè)存在直線l滿足條件,設(shè)直線l方程為y=kx+1,
由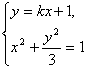 消去y得(3+k2)x2+2kx-2=0.
消去y得(3+k2)x2+2kx-2=0.
∵直線l與曲線E交于P、Q兩點(diǎn),∴Δ=4k2+8(3+k2)>0.
設(shè)P(x1,y1),Q(x2,y2),
則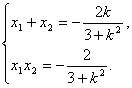
∵![]() ·
·![]() =-2,∴x1x2+y1y2=-2,
=-2,∴x1x2+y1y2=-2,
即x1x2+(kx1+1)(kx2+1)=-2,
(1+k2)x1x2+k(x1+x2)+3=0,(1+k2)(-![]() )+k(-
)+k(-![]() )+3=0,解得k2=7,k=±
)+3=0,解得k2=7,k=±![]() .
.
故存在直線l:y=±![]() +1,使得
+1,使得![]() ·
·![]() =-2.
=-2.


 星級(jí)口算天天練系列答案
星級(jí)口算天天練系列答案 芒果教輔達(dá)標(biāo)測(cè)試卷系列答案
芒果教輔達(dá)標(biāo)測(cè)試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
| OP |
| OQ |
| GD |
| GC |
| GE |
| GA |
| GF |
| GB |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
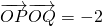 ?若存在,求出直線l的方程,若不存在,說明理由.
?若存在,求出直線l的方程,若不存在,說明理由.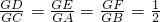 .
.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
| OP |
| OQ |
| GD |
| GC |
| GE |
| GA |
| GF |
| GB |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(1)求點(diǎn)C的軌跡E的方程;
(2)是否存在直線z,使Z過點(diǎn)(0,1)并與曲線E交于P、Q兩點(diǎn),且滿足OP⊥OQ?若存在,求出直線l的方程;若不存在,說明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com