
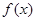 的定義域是
的定義域是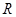 ,對于任意的
,對于任意的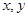 ,有
,有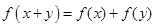 ,且當
,且當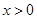 時,
時,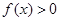 .
.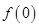 的值;
的值;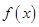 為增函數;
為增函數;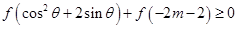 恒成立,求實數
恒成立,求實數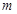 的取值范圍.
的取值范圍.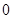 ;(2)奇函數;(3)詳見解析;(4)
;(2)奇函數;(3)詳見解析;(4)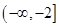 .
.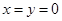 代入
代入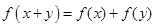 即可求出
即可求出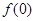 ;(2)先說明函數的定義域關于原點對稱,然后令
;(2)先說明函數的定義域關于原點對稱,然后令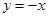 得到
得到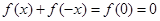 ,然后可化成
,然后可化成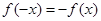 ,可判斷函數為奇函數;(3)設
,可判斷函數為奇函數;(3)設 ,則
,則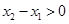 ,所以
,所以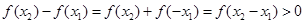 ,從而利用單調性的定義證出函數
,從而利用單調性的定義證出函數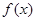 在
在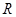 上為增函數;(4)先將不等式轉化成
上為增函數;(4)先將不等式轉化成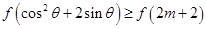 ,再由函數的單調遞增性,又轉化為
,再由函數的單調遞增性,又轉化為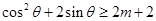 ,再分離參數得不等式
,再分離參數得不等式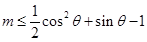 ,該不等式恒成立等價于
,該不等式恒成立等價于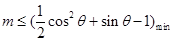 ,求出
,求出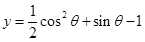 的最小值即可求出
的最小值即可求出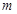 的取值范圍.
的取值范圍.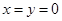 得,
得,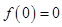 2分
2分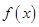 為奇函數,理由如下:已知函數的定義域為
為奇函數,理由如下:已知函數的定義域為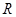
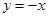 代入,得
代入,得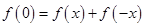 ,又
,又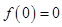 ,則
,則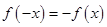
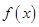 為奇函數 5分
為奇函數 5分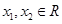 且
且 ,則
,則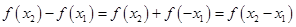
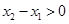 知,
知,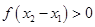 ,則
,則
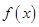 為
為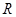 上的增函數 9分
上的增函數 9分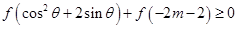 恒成立,又即
恒成立,又即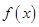 為奇函數
為奇函數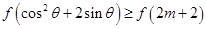 恒成立。又函數
恒成立。又函數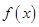 為R上的增函數
為R上的增函數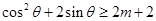 恒成立 11分
恒成立 11分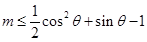 恒成立
恒成立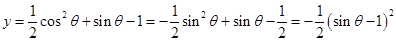
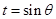 ,則
,則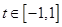 ,即
,即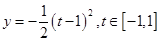 ,知
,知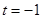 時,
時,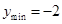
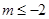 ,即實數
,即實數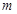 的取值范圍為
的取值范圍為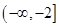 14分.
14分.

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:不詳 題型:解答題
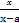 (x≠a).
(x≠a).查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.(-1,1) | B.(-1,+∞) |
| C.(-∞,-1) | D.(-∞,+∞) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com