數列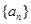
的通項
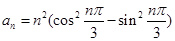，其前n項和為
．
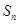（1）求
；
（2）
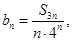求數列｛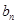
｝的前n項和
．
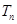（1）
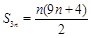；（2）
解析試題分析：（1）化簡通項公式為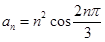
，考慮到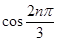
的值是周期性出現的，而且周期是3，故將數列三項并為一組為
+
+
+……+
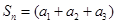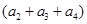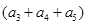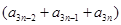分別求和，進而求；（2）求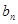
，觀察其特征選擇相應的求和方法，通常求數列前n項和的方法有①裂項相消法，在求和過程中相互抵消的辦法；②錯位相減法，通項公式是等差數列乘以等比數列的形式；③分組求和法，將數列求和問題轉化為等差數列求和或者等比數列求和問題；④奇偶并項求和法，考慮數列相鄰兩項或者相鄰幾項的特征，進而求和的方法,該題利用錯位相減法求和.
試題解析：(1) 由于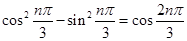
，
,∴；
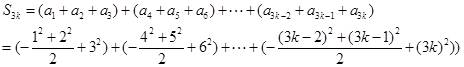
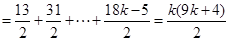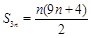(2) 
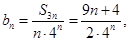
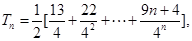
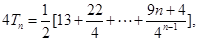
兩式相減得：
考點：1、三角函數的周期性；2、數列求和；3、余弦的二倍角公式.
一線名師提優試卷系列答案科目：高中數學 來源： 題型：解答題
正項數列{an}的前n項和Sn滿足：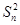
－(n2＋n－1)Sn－(n2＋n)＝0.
(1)求數列{an}的通項公式an；
(2)令bn＝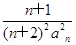
，數列{bn}的前n項和為Tn，證明：對于任意的n∈N*，都有Tn< 
.
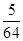查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，求證：
.
的首項
，公差
，且
分別是正數等比數列
的
項.
與
對任意
均有
成立，設
項和為
，求
的前
項和為
，且
，
，數列
滿足
，
，
；
的前
.
是單調遞增的等差數列，首項
，前
項和為
；數列
是等比數列，首項
的通項公式；
求
的前20項和
.
且
，數列
滿足
，
，
（
），令
，
是等比數列；
，求
項和
．
的各項均為正數，其前
項和為
，且
.
，求證：
；
，
，求
.
.
，求{bn}的前n項和Tn.