
已知數列 的奇數項是首項為1的等差數列,偶數項是首項為2的等比數列.數列
的奇數項是首項為1的等差數列,偶數項是首項為2的等比數列.數列 前
前 項和為
項和為 ,且滿足
,且滿足
(1)求數列 的通項公式;
的通項公式;
(2)求數列 前
前 項和
項和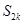 ;
;
(3)在數列 中,是否存在連續的三項
中,是否存在連續的三項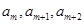 ,按原來的順序成等差數列?若存在,求出所有滿足條件的正整數
,按原來的順序成等差數列?若存在,求出所有滿足條件的正整數 的值;若不存在,說明理由
的值;若不存在,說明理由
(1)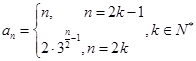 ;(2
;(2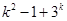 ;(3)存在,詳見解析.
;(3)存在,詳見解析.
解析試題分析:(1)此類問題一般用等差數列和等比數列的基本量根據題目條件布列方程,解之即可,體現的方程的基本思想,解出等差數列和等比數列后,便可寫出數列的通項公式,要注意本題數列的特點,可將其寫成分段的形式;(2))在求出等差數列和等比數列的公差和公比后,求得難度已經不大,但要注意分組求和;(3)此類探究性問題,一般先假設存在符合條件的連續三項,然后通過推理,求出則存在,若得到矛盾,則不存在,存在時還要注意求出所有符合條件的解,注意分類討論思想的應用.
試題解析:(1)設等差數列的公差為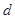 ,等比數列的公比為
,等比數列的公比為 ,
,
則

又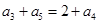 ,
,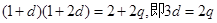 ,解得
,解得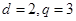
∴對于 ,有
,有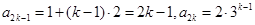
故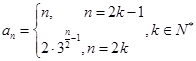 5分
5分
(2)由(1)知,在數列 中,前
中,前 項中所有奇數項的和為
項中所有奇數項的和為 ,所有偶數項的和為
,所有偶數項的和為 ,所以有
,所以有 8分
8分
(3)在數列 中,僅存在連續的三項
中,僅存在連續的三項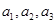 ,按原來的順序成等差數列,此時正整數
,按原來的順序成等差數列,此時正整數 的值為1,下面說明理由 10分
的值為1,下面說明理由 10分
若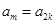 ,則由
,則由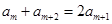 ,得
,得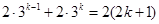
化簡得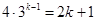 ,此式左邊為偶數,右邊為奇數,不可能成立 12分
,此式左邊為偶數,右邊為奇數,不可能成立 12分
若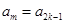 ,則由
,則由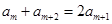 ,得
,得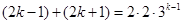
化簡得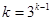 14分
14分
令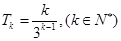 ,則
,則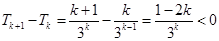
因此, ,故只有
,故只有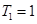 ,此時
,此時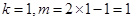
綜上,在數列 中,僅存在連續的三項
中,僅存在連續的三項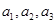 ,按原來的順序成等差數列,此時正整數
,按原來的順序成等差數列,此時正整數 的值為1 16分
的值為1 16分
考點:等差數列、等比數列,數列的求和.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
數列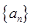 的前n項和記為Sn,a1=t,點(Sn,an+1)在直線y=2x+1上,n∈N*.
的前n項和記為Sn,a1=t,點(Sn,an+1)在直線y=2x+1上,n∈N*.
(1)當實數 為何值時,數列
為何值時,數列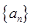 是等比數列?
是等比數列?
(2)在(1)的結論下,設 是數列
是數列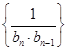 的前
的前 項和,求
項和,求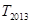 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com