
(本題滿分15分)已知函數![]()
![]() .
.
(I)討論![]() 在
在![]() 上的奇偶性;
上的奇偶性;
(II)當![]() 時,求函數
時,求函數![]() 在閉區間[-1,
在閉區間[-1,![]() ]上的最大值.
]上的最大值.
(1)f(x)是非奇非偶函數;(2)
(1)f(x)=|x|(x-a)
當a=0時,f(x)=x·|x|為奇函數
當a≠0時,f(x)=(x-a)|x|,∵f(-a)≠f(a)且f(-a)≠-f(a)
∴f(x)是非奇非偶函數
(2)當a=0時,f(x)=x|x|是奇函數,在R上單調遞增
∴當-1≤x≤![]() 時,f(-1)≤f(x)≤f(
時,f(-1)≤f(x)≤f(![]() )
)![]() f(x)∈[-1,
f(x)∈[-1,![]() ],此時f(x)max=
],此時f(x)max=![]()
當a<0時,
即
①若-1≤![]() 即a≥-2時,f(x)的最大值為f(
即a≥-2時,f(x)的最大值為f(![]() )或f(
)或f(![]() )
)
∵f(![]() )-f(
)-f(![]() )=
)=![]()
又∵-2≤a<0,則f(![]() )<f(
)<f(![]() ),∴f(
),∴f(![]() )為最大值
)為最大值
②若![]() ≤-1即a≤-2,f(x)的最大值為f(-1)或f(
≤-1即a≤-2,f(x)的最大值為f(-1)或f(![]() )
)
∵f(-1)-f(![]() )=(-1-a)-
)=(-1-a)-![]() (
(![]() -a)=-
-a)=-![]() -
-![]()
當a≤![]() 時,f(1)≥f(
時,f(1)≥f(![]() )
)
當![]() ≤a≤-2時,f(-1)≤f(
≤a≤-2時,f(-1)≤f(![]() )
)
綜上可知: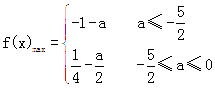


科目:高中數學 來源:2013屆浙江省余姚中學高三上學期期中考試文科數學試卷(帶解析) 題型:解答題
(本題滿分15分)已知點 (0,1),
(0,1), ,直線
,直線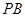 、
、 都是圓
都是圓 的切線(
的切線(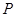 點不在
點不在 軸上).
軸上).
(Ⅰ)求過點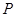 且焦點在
且焦點在 軸上的拋物線的標準方程;
軸上的拋物線的標準方程;
(Ⅱ)過點(1,0)作直線 與(Ⅰ)中的拋物線相交于
與(Ⅰ)中的拋物線相交于
 兩點,問是否存在定點
兩點,問是否存在定點 使
使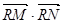 為常數?若存在,求出點
為常數?若存在,求出點 的坐標及常數;若不存在,請說明理由
的坐標及常數;若不存在,請說明理由
查看答案和解析>>
科目:高中數學 來源:2011-2012學年浙江省桐鄉市高三10月月考理科數學 題型:解答題
(本題滿分15分)已知函數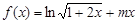 .
.
(Ⅰ)若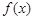 為定義域上的單調函數,求實數m的取值范圍;
為定義域上的單調函數,求實數m的取值范圍;
(Ⅱ)當 時,求函數
時,求函數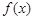 的最大值;
的最大值;
(Ⅲ)當 ,且
,且 時,證明:
時,證明: .
.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年浙江省桐鄉市高三下學期2月模擬考試文科數學 題型:解答題
(本題滿分15分)已知圓N: 和拋物線C:
和拋物線C: ,圓的切線
,圓的切線 與拋物線C交于不同的兩點A,B,
與拋物線C交于不同的兩點A,B,
(1)當直線 的斜率為1時,求線段AB的長;
的斜率為1時,求線段AB的長;
(2)設點M和點N關于直線 對稱,問是否存在直線
對稱,問是否存在直線 使得
使得 ?若存在,求出直線
?若存在,求出直線 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.

查看答案和解析>>
科目:高中數學 來源:杭州市2010年第二次高考科目教學質量檢測 題型:解答題
(本題滿分15分)已知直線 ,曲線
,曲線
(1)若 且直線與曲線恰有三個公共點時,求實數
且直線與曲線恰有三個公共點時,求實數 的取值;
的取值;
(2)若 ,直線與曲線M的交點依次為A,B,C,D四點,求|AB+|CD|的取值范圍。[來源:Z+xx+k.Com]
,直線與曲線M的交點依次為A,B,C,D四點,求|AB+|CD|的取值范圍。[來源:Z+xx+k.Com]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com