
��֪����(sh��)
 ��
��
��1��ӑՓ����(sh��) ����ż�ԣ�
����ż�ԣ�
��2��������(sh��) ��
�� �Ϟ�p����(sh��)����
�Ϟ�p����(sh��)���� ��ȡֵ������
��ȡֵ������
1����(d��ng)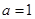 �r(sh��)��
�r(sh��)�� ���溯��(sh��)����(d��ng)
���溯��(sh��)����(d��ng)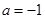 �r(sh��)��
�r(sh��)�� ��ż����(sh��)����(d��ng)
��ż����(sh��)����(d��ng)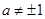 �r(sh��)��
�r(sh��)�� �Ƿ����ż����(sh��)����2��
�Ƿ����ż����(sh��)����2��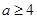 .
.
����ԇ�}��������1���о�����(sh��)��ż�ԣ������о����x��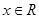 ���ڶ��x��ǰ���£��о�
���ڶ��x��ǰ���£��о�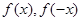 ��Ȼ��෴�P(gu��n)ϵ. ��
��Ȼ��෴�P(gu��n)ϵ. ��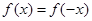 ���t
���t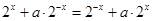 ��
��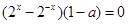 ��
��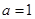 ����
����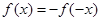 ��
��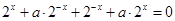 ��
��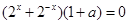 ��
��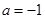 ,��2�����ú���(sh��)���{(di��o)�Զ��x�о�����(sh��)���{(di��o)��. ��(sh��)
,��2�����ú���(sh��)���{(di��o)�Զ��x�о�����(sh��)���{(di��o)��. ��(sh��) ��
�� �Ϟ�p����(sh��)���ʌ�(du��)�����
�Ϟ�p����(sh��)���ʌ�(du��)����� ������
������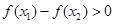 ����
����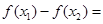
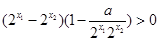 �������
�������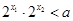 ���������?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/b9/9/q0llh.png" style="vertical-align:middle;" />������
���������?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/b9/9/q0llh.png" style="vertical-align:middle;" />������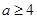 .
.
��1��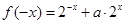 ��1�֣�
��1�֣�
�� ��ż����(sh��)���t��(du��)�����
��ż����(sh��)���t��(du��)�����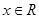 ������
������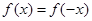 ��
��
��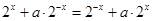 ��
��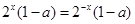 ��
��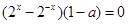 ��(du��)�����
��(du��)�����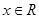 ������������
������������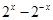 �������0������
�������0������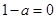 ����
����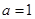 �ஔ(d��ng)
�ஔ(d��ng)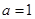 �r(sh��)��
�r(sh��)�� ��ż����(sh��)�� ��4�֣�
��ż����(sh��)�� ��4�֣�
�� ���溯��(sh��)���t��(du��)�����
���溯��(sh��)���t��(du��)�����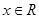 ������
������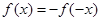 ��
��
��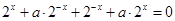 ��
��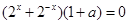 ��(du��)�����
��(du��)�����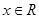 ������������
������������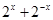 �������0������
�������0������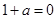 ����
����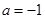 �ஔ(d��ng)
�ஔ(d��ng)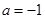 �r(sh��)��
�r(sh��)�� ���溯��(sh��)�� ��6�֣�
���溯��(sh��)�� ��6�֣�
�ஔ(d��ng)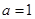 �r(sh��)��
�r(sh��)�� ���溯��(sh��)����(d��ng)
���溯��(sh��)����(d��ng)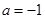 �r(sh��)��
�r(sh��)�� ��ż����(sh��)����(d��ng)
��ż����(sh��)����(d��ng)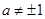 �r(sh��)��
�r(sh��)�� �Ƿ����ż����(sh��)�� ��7�֣�
�Ƿ����ż����(sh��)�� ��7�֣�
��2����(sh��) ��
�� �Ϟ�p����(sh��)���ʌ�(du��)�����
�Ϟ�p����(sh��)���ʌ�(du��)����� ������
������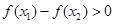 �� ��2�֣�
�� ��2�֣�
��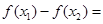
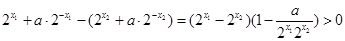 ������� ��4�֣���
������� ��4�֣���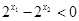 ��֪
��֪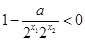 ���������
���������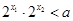 �������
�������
���ڮ�(d��ng) �r(sh��)
�r(sh��)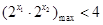 ��6�֣�
��6�֣�
��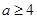 ��7�֣�
��7�֣�
���c(di��n)������(sh��)��ż���c���{(di��o)��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪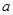 �錍(sh��)��(sh��)��
�錍(sh��)��(sh��)��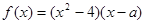 ��
��
��1����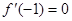 ����
���� ��
��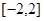 �ϵ����ֵ����Сֵ��
�ϵ����ֵ����Сֵ��
��2���� ��
��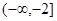 ��
��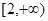 �϶����f���ģ���
�϶����f���ģ���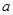 ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
ij�̈�(ch��ng)�N(xi��o)��ij�N��Ʒ�Ľ�(j��ng)�(y��n)������ԓ��Ʒÿ�յ��N(xi��o)����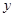 ����λ��ǧ�ˣ��c�N(xi��o)�ۃr(ji��)��
����λ��ǧ�ˣ��c�N(xi��o)�ۃr(ji��)��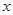 ����λ��Ԫ/ǧ�ˣ��M(m��n)���P(gu��n)ϵʽ
����λ��Ԫ/ǧ�ˣ��M(m��n)���P(gu��n)ϵʽ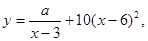 ����
����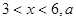 �鳣��(sh��)����֪�N(xi��o)�ۃr(ji��)���5Ԫ/ǧ�˕r(sh��)��ÿ�տ��۳�ԓ��Ʒ11ǧ�ˣ�
�鳣��(sh��)����֪�N(xi��o)�ۃr(ji��)���5Ԫ/ǧ�˕r(sh��)��ÿ�տ��۳�ԓ��Ʒ11ǧ�ˣ�
��1���� ��ֵ��
��ֵ��
��2����ԓ��Ʒ�ijɱ���3Ԫ/ǧ�ˣ�ԇ�_���N(xi��o)�ۃr(ji��)��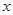 ��ֵ��ʹ�̈�(ch��ng)ÿ���N(xi��o)��ԓ��Ʒ���@�õ�����(r��n)���
��ֵ��ʹ�̈�(ch��ng)ÿ���N(xi��o)��ԓ��Ʒ���@�õ�����(r��n)���
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪����(sh��)f(x)��2x��x��R.��(d��ng)mȡ��ֵ�r(sh��)����|f(x)��2|��m��һ��(g��)�⣿?j��)ɂ�(g��)�⣿
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
���x����(sh��)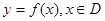 (
( �鶨�x��)�D���ϵ��c(di��n)������(bi��o)ԭ�c(di��n)�ľ��x�麯��(sh��)��
�鶨�x��)�D���ϵ��c(di��n)������(bi��o)ԭ�c(di��n)�ľ��x�麯��(sh��)��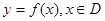 ��ģ.��ģ�������ֵ���t�Q(ch��ng)֮�麯��(sh��)
��ģ.��ģ�������ֵ���t�Q(ch��ng)֮�麯��(sh��)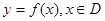 ���L(zh��ng)�ࣻ��ģ������Сֵ���t�Q(ch��ng)֮�麯��(sh��)
���L(zh��ng)�ࣻ��ģ������Сֵ���t�Q(ch��ng)֮�麯��(sh��)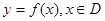 �Ķ̾�.
�Ķ̾�.
(1)�քe�Дຯ��(sh��)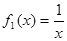 �c
�c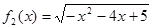 �Ƿ�����L(zh��ng)���c�̾࣬�����ڣ�Ո(q��ng)���;
�Ƿ�����L(zh��ng)���c�̾࣬�����ڣ�Ո(q��ng)���;
(2)���C��ָ��(sh��)����(sh��)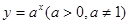 �Ķ̾�С��1;
�Ķ̾�С��1;
(3)��(du��)������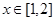 �Ƿ���ڌ�(sh��)��(sh��)
�Ƿ���ڌ�(sh��)��(sh��)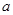 ��ʹ�ú���(sh��)
��ʹ�ú���(sh��)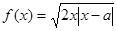 �Ķ̾С��2���L(zh��ng)�����4.�����ڣ�Ո(q��ng)���
�Ķ̾С��2���L(zh��ng)�����4.�����ڣ�Ո(q��ng)���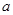 ��ȡֵ�����������ڣ��t�f(shu��)�����ɣ�
��ȡֵ�����������ڣ��t�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�O(sh��)����(sh��) ��
�У� ���攵(sh��)��
���攵(sh��)�� ��������(sh��)����
��������(sh��)���� �����攵(sh��).���C��
�����攵(sh��).���C�� �o(w��)����(sh��)����
�o(w��)����(sh��)����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪ �Ƕ��κ���(sh��)������ʽ
�Ƕ��κ���(sh��)������ʽ �Ľ⼯��(0��5)����
�Ľ⼯��(0��5)���� �څ^(q��)�g[-1��4]�ϵ����ֵ��12��
�څ^(q��)�g[-1��4]�ϵ����ֵ��12��
��1����f(x)�Ľ���ʽ��
��2���Ƿ����������(sh��)m,ʹ�÷��� �څ^(q��)�g
�څ^(q��)�g ��(n��i)����ֻ�Ѓɂ�(g��)���ȵČ�(sh��)��(sh��)���������ڣ��������m��ֵ���������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
��(n��i)����ֻ�Ѓɂ�(g��)���ȵČ�(sh��)��(sh��)���������ڣ��������m��ֵ���������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��(j��)�h(hu��n)�����T(m��n)�y(c��)����ij̎����Ⱦָ��(sh��)�c������ȾԴ�ď�(qi��ng)�ȳ����ȣ��c����ȾԴ���x��ƽ���ɷ��ȣ���������(sh��)��
 ���F(xi��n)��֪���18
���F(xi��n)��֪���18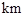 ��A��B�ɼһ����S(ch��ng)����ȾԴ������Ⱦ��(qi��ng)�ȷքe��
��A��B�ɼһ����S(ch��ng)����ȾԴ������Ⱦ��(qi��ng)�ȷքe�� �������B��(xi��n)������һ�c(di��n)C̎����Ⱦָ��(sh��)
�������B��(xi��n)������һ�c(di��n)C̎����Ⱦָ��(sh��) ���ڃɻ����S(ch��ng)��(du��)ԓ̎����Ⱦָ��(sh��)֮�ͣ��O(sh��)
���ڃɻ����S(ch��ng)��(du��)ԓ̎����Ⱦָ��(sh��)֮�ͣ��O(sh��) ��
��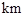 ����
����
��1��ԇ�� ��ʾ��
��ʾ�� �ĺ���(sh��)�� ��2����
���(sh��)�� ��2���� ����
���� �r(sh��)��
�r(sh��)�� ȡ����Сֵ��ԇ��
ȡ����Сֵ��ԇ�� ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
���x����(du��)�ں���(sh��) �������ڷ��㳣��(sh��)
�������ڷ��㳣��(sh��) ��ʹ����(sh��)
��ʹ����(sh��) ��(du��)�ڶ��x���(n��i)�����⌍(sh��)��(sh��)
��(du��)�ڶ��x���(n��i)�����⌍(sh��)��(sh��) ������
������ ���t�Q(ch��ng)����(sh��)
���t�Q(ch��ng)����(sh��) �ǏV�x���ں���(sh��)�����зQ(ch��ng)
�ǏV�x���ں���(sh��)�����зQ(ch��ng) �麯��(sh��)
�麯��(sh��) �ďV�x���ڣ�
�ďV�x���ڣ� �Q(ch��ng)���ܾ࣮
�Q(ch��ng)���ܾ࣮
��1���C������(sh��) ����2��V�x���ڵďV�x���ں���(sh��)���������������(y��ng)�ܾ�
����2��V�x���ڵďV�x���ں���(sh��)���������������(y��ng)�ܾ� ��ֵ��
��ֵ��
��2��ԇ��һ��(g��)����(sh��) ��ʹ
��ʹ ��
�� �鳣��(sh��)��
�鳣��(sh��)�� ����V�x���ں���(sh��)�����������һ��(g��)�V�x����
����V�x���ں���(sh��)�����������һ��(g��)�V�x���� ���ܾ�
���ܾ� ��
��
��3���O(sh��)����(sh��) ������
������ �����ں���(sh��)����(d��ng)����(sh��)
�����ں���(sh��)����(d��ng)����(sh��) ��
�� �ϵ�ֵ��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/4a/9/1ybvn2.png" style="vertical-align:middle;" />�r(sh��)����
�ϵ�ֵ��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/4a/9/1ybvn2.png" style="vertical-align:middle;" />�r(sh��)���� ��
�� �ϵ����ֵ����Сֵ��
�ϵ����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com