
(本小題共14分)
在單調遞增數列 中,
中, ,不等式
,不等式
 對任意
對任意 都成立.
都成立.
(Ⅰ)求 的取值范圍;
的取值范圍;
(Ⅱ)判斷數列 能否為等比數列?說明理由;
能否為等比數列?說明理由;
(Ⅲ)設 ,
, ,求證:對任意的
,求證:對任意的 ,
, .
.
(1)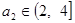 (2) 用反證法證明:假設數列
(2) 用反證法證明:假設數列 是公比為
是公比為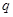 的等比數列, 因為
的等比數列, 因為 單調遞增,所以
單調遞增,所以 .因為
.因為 ,
,
 都成立,從而加以證明。
都成立,從而加以證明。
(3)通過前幾項歸納猜想,然后運用數學歸納法加以證明。
解析試題分析:(Ⅰ)解:因為 是單調遞增數列,
是單調遞增數列,
所以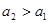 ,
,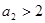 .
.
令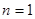 ,
,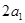
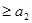 ,
,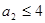 ,
,
所以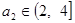 . ………………4分
. ………………4分
(Ⅱ)證明:數列 不能為等比數列.
不能為等比數列.
用反證法證明:
假設數列 是公比為
是公比為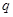 的等比數列,
的等比數列,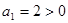 ,
,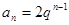 .
.
因為 單調遞增,所以
單調遞增,所以 .
.
因為 ,
,
 都成立.
都成立.
所以 ,
,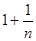
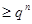 ①
①
因為 ,所以
,所以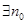
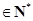 ,使得當
,使得當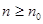 時,
時,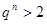 .
.
因為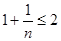
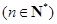 .
.
所以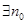
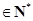 ,當
,當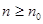 時,
時,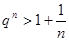 ,與①矛盾,故假設不成立.………9分
,與①矛盾,故假設不成立.………9分
(Ⅲ)證明:觀察: 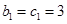 ,
,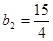
 ,
,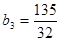
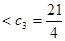 ,…,猜想:
,…,猜想: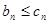 .
.
用數學歸納法證明:
(1)當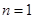 時,
時,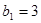
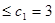 成立;
成立;
(2)假設當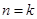 時,
時,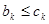 成立;
成立;
當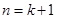 時,
時,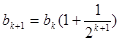
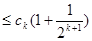
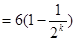

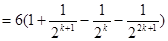
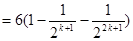

所以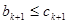 .
.
根據(1)(2)可知,對任意 ,都有
,都有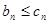 ,即
,即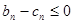 .
.
由已知得,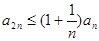 .
.
所以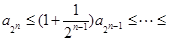
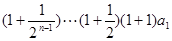 .
.
所以當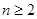 時,
時,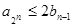
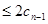
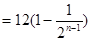
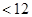 .
.
因為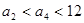 .
.
所以對任意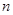
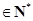 ,
,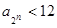 .
.
對任意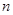
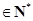 ,存在
,存在
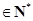 ,使得
,使得 ,
,
因為數列{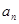


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
(本題滿分16分)
已知數列 ,其中
,其中 是首項為1,公差為1的等差數列;
是首項為1,公差為1的等差數列; 是公差為
是公差為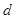 的等差數列;
的等差數列; 是公差為
是公差為 的等差數列(
的等差數列( ).
).
(Ⅰ)若 = 30,求
= 30,求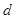 ;
;
(Ⅱ)試寫出a30關于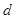 的關系式,并求a30的取值范圍;
的關系式,并求a30的取值范圍;
(Ⅲ)續寫已知數列,可以使得 是公差為
是公差為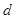 3的等差數列,請你依次類推,把已知數列推廣為無窮數列,試寫出
3的等差數列,請你依次類推,把已知數列推廣為無窮數列,試寫出 關于
關于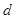 的關系式(
的關系式( N
N );
);
(Ⅳ)在(Ⅲ)條件下,且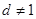 ,試用
,試用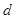 表示此數列的前100項和
表示此數列的前100項和
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
把正奇數數列 中的數按上小下大、左小右大的原則排成如下三角形數表:
中的數按上小下大、左小右大的原則排成如下三角形數表:
1
3 5
7 9 11
………………………
……………………………
設
 是位于這個三角形數表中從上往下數第
是位于這個三角形數表中從上往下數第 行、從左往右數第
行、從左往右數第 個數.
個數.
(1)若 ,求
,求 的值;
的值;
(2)若記三角形數表中從上往下數第 行各數的和為
行各數的和為 ,求證
,求證 .(本題滿分14分)
.(本題滿分14分)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com