
已知函數 .
.
(1)求證函數 在區間
在區間 上存在唯一的極值點,并用二分法求函數取得極值時相應
上存在唯一的極值點,并用二分法求函數取得極值時相應 的近似值(誤差不超過
的近似值(誤差不超過 );(參考數據
);(參考數據 ,
, ,
, )
)
(2)當 時,若關于
時,若關于 的不等式
的不等式 恒成立,試求實數
恒成立,試求實數 的取值范圍.
的取值范圍.
解:(Ⅰ)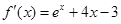 , ∵
, ∵ 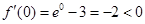 ,
,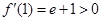 ,
,
∴ 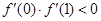 .
……………………2分
.
……………………2分
令 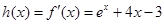 ,則
,則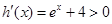 , ……………………3分
, ……………………3分
∴ 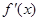 在區間
在區間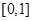 上單調遞增,∴
上單調遞增,∴ 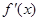 在區間
在區間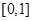 上存在唯一零點,
上存在唯一零點,
∴ 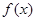 在區間
在區間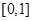 上存在唯一的極小值點. …………………………………4分
上存在唯一的極小值點. …………………………………4分
取區間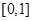 作為起始區間,用二分法逐次計算如下:
作為起始區間,用二分法逐次計算如下:
 ,而
,而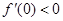 ,∴ 極值點所在區間是
,∴ 極值點所在區間是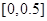 ;
;
又 ,∴ 極值點所在區間是
,∴ 極值點所在區間是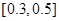 ;
;
③ ∵ 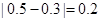 ,∴ 區間
,∴ 區間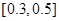 內任意一點即為所求. ……7分
內任意一點即為所求. ……7分
(Ⅱ)由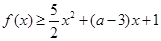 ,得
,得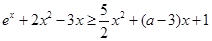 ,
,
即 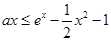 ,∵
,∵ 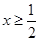 , ∴
, ∴ 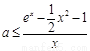 ,……………………8分
,……………………8分
令 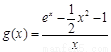 , 則
, 則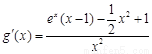 . ………………10分
. ………………10分
令 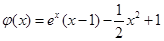 ,則
,則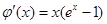 .
.
∵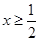 ,∴
,∴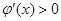 ,∴
,∴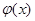 在
在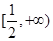 上單調遞增,∴
上單調遞增,∴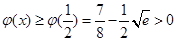 ,
,
因此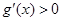 故
故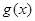 在
在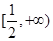 上單調遞增,
……………………12分
上單調遞增,
……………………12分
則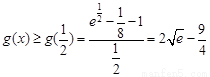 ,∴
,∴ 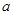 的取值范圍是
的取值范圍是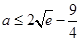 ………13分
………13分
【解析】略


科目:高中數學 來源:2011-2012學年人教版高一(上)期中數學試卷(解析版) 題型:解答題
 .
. 在(0,+∞)上是減函數.
在(0,+∞)上是減函數.查看答案和解析>>
科目:高中數學 來源:2010年上海市奉賢區高考數學二模試卷(文科)(解析版) 題型:解答題
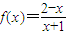 ;
; 成立,若存在求出x;若不存在,請說明理由.
成立,若存在求出x;若不存在,請說明理由.查看答案和解析>>
科目:高中數學 來源:2013屆浙江省高二下期中數學試卷(解析版) 題型:解答題
已知函數 令
令
(1)求 的定義域;
的定義域;
(2)判斷函數 的奇偶性,并予以證明;
的奇偶性,并予以證明;
(3)若 ,猜想
,猜想 之間的關系并證明.
之間的關系并證明.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年北京市高三入學測試數學卷 題型:解答題
(本小題滿分12分)
已知函數 ,
,
(1)求函數 的定義域;(2)證明:
的定義域;(2)證明: 是偶函數;
是偶函數;
(3)若 ,求
,求 的取值范圍。
的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com