
已知函數y=f(x)是定義在區間[- ,
, ]上的偶函數,且
]上的偶函數,且
x∈[0, ]時,
]時,
(1)求函數f(x)的解析式;
(2)若矩形ABCD的頂點A,B在函數y=f(x)的圖像上,頂點C,D在x軸上,求矩形ABCD面積的最大值.
(1)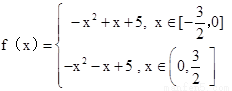 (2)6
(2)6
【解析】本題主要考查了分段函數、函數的最值及其幾何意義及利用導數研究函數的極值,屬于中檔題.
(1)欲求函數f(x)的解析式,只須求出函數f(x)在x∈[-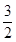 ,0]時的解析式即可,利用函數的偶函數性質即可由y軸右側的表達式求出在y軸左側的表達式.最后利用分段函數寫出解析式即可.
,0]時的解析式即可,利用函數的偶函數性質即可由y軸右側的表達式求出在y軸左側的表達式.最后利用分段函數寫出解析式即可.
(2)設A點在第一象限,坐標為A(t,-t2-t+5),利用對稱性求出B點坐標,進而求出矩形ABCD面積,最后利用導數求出此面積表達式的最大值即可.
解(1)當x∈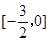 時,-x∈
時,-x∈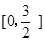 .
.
∴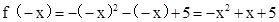 .又∵f(x)是偶函數,
.又∵f(x)是偶函數,
∴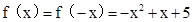 .
.
∴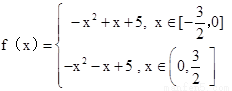 .
.
(2)由題意,不妨設A點在第一象限,
坐標為(t,-t2-t+5),其中t∈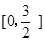
由圖象對稱性可知B點坐標為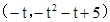 .
.
則S(t)= 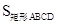 =
=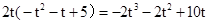
s′(t)=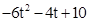 .由s′(t)=0,得
.由s′(t)=0,得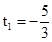 (舍去),
(舍去),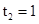 .
.
當0<t<1時,s′(t)>0;t>1時,s′(t)<0.
∴S(t)在(0,1]上單調遞增,在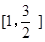 上單調遞減.
上單調遞減.
∴當t=1時,矩形ABCD的面積取得極大值6,
且此極大值也是S(t)在t∈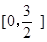 上的最大值.
上的最大值.
從而當t=1時,矩形ABCD的面積取得最大值6.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2011 |
| 2 |
| 2011 |
| 3 |
| 2011 |
| 4 |
| 2011 |
| 2010 |
| 2011 |
| A、1005 | B、2010 |
| C、2011 | D、4020 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| lnx |
| x |
| 1 |
| e |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1-x | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com