
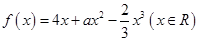 在區間
在區間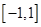 上是增函數.
上是增函數.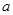 的值組成的集合
的值組成的集合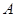 ;
;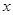 的方程
的方程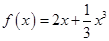 的兩個非零實根為
的兩個非零實根為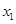 、
、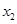 .試問:是否存在實數
.試問:是否存在實數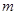 ,使得不等式
,使得不等式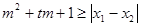 對任意
對任意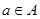 及
及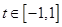 恒成立?若存在,求
恒成立?若存在,求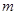 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.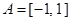 ;
; ,使得不等式
,使得不等式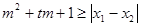 對任意
對任意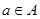 及
及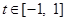 恒成立.
恒成立. 的導數
的導數 ,將條件
,將條件 在區間
在區間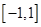 上為增函數這一條件轉化為
上為增函數這一條件轉化為 在區間
在區間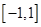 上恒成立,結合二次函數的圖象得到
上恒成立,結合二次函數的圖象得到 ,從而解出實數
,從而解出實數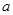 的取值范圍;(2)先將方程
的取值范圍;(2)先將方程 轉化為一元二次方程,結合韋達定理得到
轉化為一元二次方程,結合韋達定理得到 與
與 ,然后利用
,然后利用
 將
將 用參數
用參數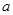 進行表示,進而得到不等式
進行表示,進而得到不等式 對任意
對任意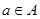
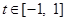 恒成立,等價轉化為
恒成立,等價轉化為 對任意
對任意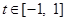 恒成立,將不等式
恒成立,將不等式 轉化為以
轉化為以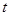 為自變量的一次函數不等式恒成立,只需考慮相應的端點值即可,從而解出參數
為自變量的一次函數不等式恒成立,只需考慮相應的端點值即可,從而解出參數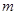 的取值范圍.
的取值范圍.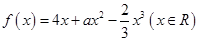 在區間
在區間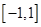 上是增函數,
上是增函數, 在區間
在區間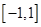 上恒成立,
上恒成立, ,
,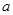 的值組成的集合
的值組成的集合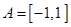 ;
;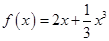 得
得 ,即
,即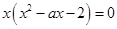 ,
,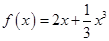 ,即
,即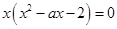 的兩個非零實根為
的兩個非零實根為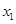 、
、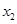 ,
, 、
、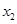 是方程
是方程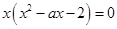 兩個非零實根,于是
兩個非零實根,于是 ,
,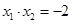 ,
,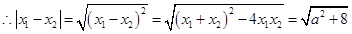 ,
,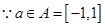 ,
, ,
,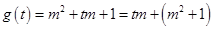 ,
,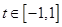 ,
, ,
, 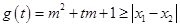 對任意
對任意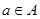 及
及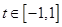 恒成立,
恒成立, ,解得
,解得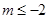 或
或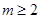 ,
,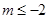 或
或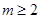 ,使得不等式
,使得不等式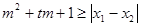 對任意
對任意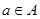 及
及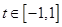 恒成立.
恒成立.

 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com