
(1) ![]() +
+![]() =3
=3![]() -
-![]() ;?
;?
(2) ![]() =4
=4![]() -
-![]() -
-![]() .?
.?
解法一:(1)原式可變形為
![]() =
=![]() +(
+(![]() -
-![]() )+(
)+(![]() -
-![]() )=
)= ![]() +
+![]() +
+![]() .?
.?
由共面向量定理的推論知P與A、B、M?共面?.?
(2)原式可變形為![]() =2
=2![]() +
+![]() -
-![]() +
+![]() -
-![]()
=2![]() +
+![]() +
+![]() .
.
由共面向量定理的推論可得
P位于平面ABM內的充要條件可寫成![]() =
=![]() +x
+x![]() +y
+y![]() .
.
而此題推得![]() =2
=2![]() +
+![]() +
+![]() ,?
,?
∴P與A、B、M不共面.?
解法二:(1)原式可變形為
![]() =3
=3![]() -
-![]() -
-![]() .?
.?
∵3+(-1)+(-1)=1,?
∴B與P、A、M共面,?
即P與A、B、M共面.?
(2)![]() =4
=4![]() -
-![]() -
-![]() ,
,
∵4+(-1)+(-1)=2≠1,?
∴P與A、B、M不共面.?
溫馨提示:判斷點P是否位于平面MAB內,關鍵是看向量![]() 能否用向量
能否用向量![]() 、
、![]() 表示(或看向量
表示(或看向量![]() 是否能寫成
是否能寫成![]() +x
+x![]() +y
+y![]() 的形式).當
的形式).當![]() 能用
能用![]() 、
、![]() 表示時,P位于平面MAB內;當
表示時,P位于平面MAB內;當![]() 不能用
不能用![]() 、
、![]() 表示時,P不在平面MAB內.當
表示時,P不在平面MAB內.當![]() =x
=x![]() +?y
+?y![]() +z
+z![]() 時,P與M、A、B共面的充要條件是x+ y+ z=1.本例利用這個結論判斷P與M、A、B是否共面更簡便.
時,P與M、A、B共面的充要條件是x+ y+ z=1.本例利用這個結論判斷P與M、A、B是否共面更簡便.


 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案 學習實踐園地系列答案
學習實踐園地系列答案科目:高中數學 來源:設計選修數學2-1蘇教版 蘇教版 題型:044
已知A、B、M三點不共線,對于平面ABM外的任一點O,確定下列各條件下,點P是否與A、B、M一定共面.
(1)![]() +
+![]() =3
=3![]() -
-![]() ;
;
(2)![]() =4
=4![]() -
-![]() -
-![]() .
.
查看答案和解析>>
科目:高中數學 來源:2011-2012年湖南省衡陽市高二第三次月考考試理科數學 題型:選擇題
已知A、B、M三點不共線,對于平面ABM外任一點O,若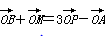 ,則點P與A、B、M( )
,則點P與A、B、M( )
A.共面 B.共線
C.不共面 D.不確定
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com