
已知橢圓![]() ,直線l:
,直線l:![]() ,P點是l上一點,射線OP交橢圓于點R,又點Q在OP上且滿足
,P點是l上一點,射線OP交橢圓于點R,又點Q在OP上且滿足![]() 。當點P在l上移動時,求點Q的軌跡方程。
。當點P在l上移動時,求點Q的軌跡方程。
解法一:設Q![]() ,Q點不在原點,
,Q點不在原點,![]()
顯然x,y不同是為零
①P點不在y軸時,即![]() 時
時
∵ R不在橢圓上
∴ 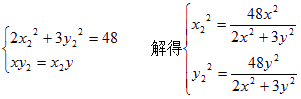
又∵ ![]()
∵ P點在直線l上,∴ 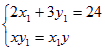
解得: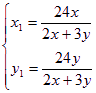
∵ ![]()
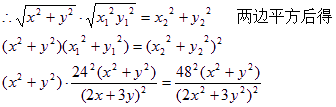
∵ x、y不同時為零
∴ ![]()
∵ Q點與坐標原點O在直線l的同側
∴ ![]()
則:![]()
即:![]()
②P點在y軸上時,P(0,8)
k(0,4)
![]() 可得Q(0,2),Q點滿足這個方程
可得Q(0,2),Q點滿足這個方程
∴ 所求的軌跡方程是![]()
|
|
解法二:點的坐標同上,過P、R、Q分別作y軸的垂線,垂足分別記作![]()
∵ ![]()
又∵ ![]()
∴ ![]()
即 ![]()
由題已知 ![]() 三個量同號
三個量同號
∴ ![]()
設 射線OP方程為![]()
則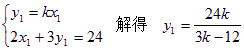
又R也在OP上,∴ 
代入![]() 中
中
![]()
![]()
化簡: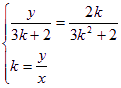

∵ ![]()
則![]() 為所求的軌跡方程
為所求的軌跡方程
本題動點Q的運動依賴于①P點的運動。②![]() 這樣兩個關系,又O、Q、R、P、D點共線,可以把P點、R點的坐標分別用動點Q的坐標表示后一起代入③④⑤
這樣兩個關系,又O、Q、R、P、D點共線,可以把P點、R點的坐標分別用動點Q的坐標表示后一起代入③④⑤ ![]() 中去整理。化簡得軌跡方程;另外也可以過Q、R、P三點分別做y軸的垂線,將
中去整理。化簡得軌跡方程;另外也可以過Q、R、P三點分別做y軸的垂線,將![]() 轉化成這三點縱坐標的關系,再求軌跡方程。本題解法一仍是坐標代換法的一種形式,主要是將動點的相關點的坐標用動點坐標表示后,代入聯系著它們的等式中,求出動點的軌跡方程,這里因P點在直線l:
轉化成這三點縱坐標的關系,再求軌跡方程。本題解法一仍是坐標代換法的一種形式,主要是將動點的相關點的坐標用動點坐標表示后,代入聯系著它們的等式中,求出動點的軌跡方程,這里因P點在直線l:![]() 上運動,而該直線與y軸可以相交,當P點在 y軸上時,R、Q也相對確定成為定值,所以在解決這個問題時,先兩步,第一部P在直線l上,運動不在y軸時(完全是“動態”)情況,第二步必須再看P在y軸時Q點做為定點是否符合所求的軌跡方程。這正是容易被忽略的,必須注意。
上運動,而該直線與y軸可以相交,當P點在 y軸上時,R、Q也相對確定成為定值,所以在解決這個問題時,先兩步,第一部P在直線l上,運動不在y軸時(完全是“動態”)情況,第二步必須再看P在y軸時Q點做為定點是否符合所求的軌跡方程。這正是容易被忽略的,必須注意。
綜上,在圓錐曲線的標準方程這部分內容中,應掌握的求曲線方程的基本方法。由于求曲線方程是平面解析幾何兩個主要內容之一,可以題型多,方法多。但因為坐標軸平移還沒學到因而涉及到園錐曲線的一般式的問題后再講。


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2014屆湖北孝感高級中學高二上學期期末考試理科數學試卷(解析版) 題型:解答題
已知橢圓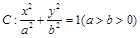 ,直線l為圓
,直線l為圓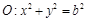 的一條切線,且經過橢圓C的右焦點,直線l的傾斜角為
的一條切線,且經過橢圓C的右焦點,直線l的傾斜角為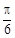 ,記橢圓C的離心率為e.
,記橢圓C的離心率為e.
(1)求e的值;
(2)試判定原點關于l的對稱點是否在橢圓上,并說明理由。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年北京市高三壓軸文科數學試卷(解析版) 題型:解答題
(本小題共13分)
已知橢圓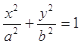
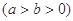 和直線L:
和直線L: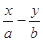 =1, 橢圓的離心率
=1, 橢圓的離心率 ,直線L與坐標原點的距離為
,直線L與坐標原點的距離為 。
。
(1)求橢圓的方程;
(2)已知定點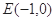 ,若直線
,若直線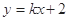
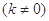 與橢圓相交于C、D兩點,試判斷是否存在
與橢圓相交于C、D兩點,試判斷是否存在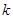 值,使以CD為直徑的圓過定點E?若存在求出這個
值,使以CD為直徑的圓過定點E?若存在求出這個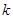 值,若不存在說明理由。
值,若不存在說明理由。
查看答案和解析>>
科目:高中數學 來源:2010-2011學年黑龍江省高三上學期期末考試數學理卷 題型:解答題
(12分)已知橢圓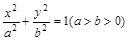 ,直線l與橢圓交于A、B兩點,M是線段AB的中點,連接OM并延長交橢圓于點C.直線AB與直線OM的斜率分別為k、m,且
,直線l與橢圓交于A、B兩點,M是線段AB的中點,連接OM并延長交橢圓于點C.直線AB與直線OM的斜率分別為k、m,且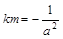 .
.

(Ⅰ)求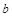 的值;
的值;
(Ⅱ)若直線AB經過橢圓的右焦點F,問:對于任意給定的不等于零的實數k,是否存在a∈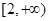 ,使得四邊形OACB是平行四邊形,請證明你的結論;
,使得四邊形OACB是平行四邊形,請證明你的結論;
查看答案和解析>>
科目:高中數學 來源:2008-2009學年福建省泉州市南安一中高二(上)年期末數學試卷(文科)(解析版) 題型:解答題
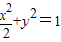 及直線l:y=x+m.
及直線l:y=x+m.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com