
(本小題滿分12分)
在△ABC中,已知b= ,c=1,∠B=60°,求a和∠A,∠C.
,c=1,∠B=60°,求a和∠A,∠C.
 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案科目:高中數學 來源: 題型:解答題
(本題滿分12分)
如圖,甲船以每小時30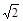 海里的速度向正北方向航行,乙船按固定方向勻速直線航行.當甲船位于A1處時,乙船位于甲船的北偏西105°方向的B1處,此時兩船相距20海里.當甲船航行20分鐘到達A2處時,乙船航行到甲船的北偏西120°方向的B2處,此時兩船相距10
海里的速度向正北方向航行,乙船按固定方向勻速直線航行.當甲船位于A1處時,乙船位于甲船的北偏西105°方向的B1處,此時兩船相距20海里.當甲船航行20分鐘到達A2處時,乙船航行到甲船的北偏西120°方向的B2處,此時兩船相距10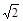 海里,問乙船每小時航行多少海里?
海里,問乙船每小時航行多少海里?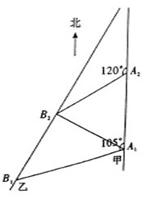
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,某觀測站C在城A的南偏西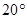 的方向,從城A出發有一條走向為南偏東
的方向,從城A出發有一條走向為南偏東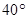 的公路,在C處觀測到距離C處31km的公路上的B處有一輛汽車正沿公路向A城駛去,行駛了20km后到達D處,測得C,D兩處的距離為21km,這時此車距離A城多少千米?
的公路,在C處觀測到距離C處31km的公路上的B處有一輛汽車正沿公路向A城駛去,行駛了20km后到達D處,測得C,D兩處的距離為21km,這時此車距離A城多少千米?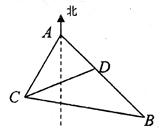
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com