
題目列表(包括答案和解析)
(13) 設(shè)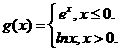 則
則 __________
__________
[解析]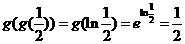 .
.
[點(diǎn)評(píng)]本題考察了分段函數(shù)的表達(dá)式、指對(duì)數(shù)的運(yùn)算.
(14) 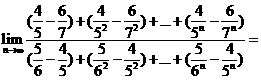 _____________
_____________
[解析]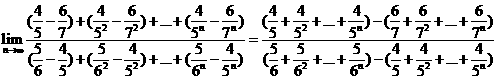
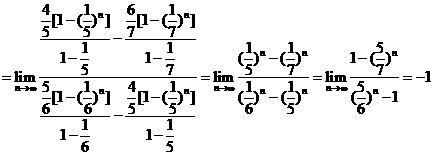
[點(diǎn)評(píng)]本題考查了等比數(shù)列的求和公式以及數(shù)列極限的基本類型.
(15) 5名乒乓球隊(duì)員中,有2名老隊(duì)員和3名新隊(duì)員.現(xiàn)從中選出3名隊(duì)員排成1、2、3號(hào)參加團(tuán)體比賽,則入選的3名隊(duì)員中至少有一名老隊(duì)員,且1、2號(hào)中至少有1名新隊(duì)員的排法有_______種.(以數(shù)作答)
[解析]兩老一新時(shí), 有 種排法;
種排法;
兩新一老時(shí), 有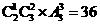 種排法,即共有48種排法.
種排法,即共有48種排法.
[點(diǎn)評(píng)]本題考查了有限制條件的排列組合問(wèn)題以及分類討論思想.
(16) 若一條直線與一個(gè)正四棱柱各個(gè)面所成的角都為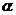 ,則
,則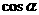 =______
=______
[解析]不妨認(rèn)為一個(gè)正四棱柱為正方體,與正方體的所有面成角相等時(shí),為與相交于同一頂點(diǎn)的三個(gè)相互垂直的平面所成角相等,即為體對(duì)角線與該正方體所成角.故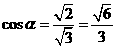 .
.
[點(diǎn)評(píng)]本題考查了直線與平面所成角的定義以及正四棱柱的概念,充分考查了轉(zhuǎn)化思想的應(yīng)用.
22.(本小題滿分12分)
已知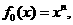
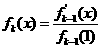 ,其中
,其中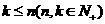 ,設(shè)
,設(shè) ,
,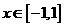 .
.
(I) 寫出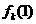 ;
;
(II) 證明:對(duì)任意的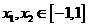 ,恒有
,恒有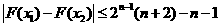 .
.
高考試題理科數(shù)學(xué)試題
(17) (本小題滿分12分)
已知函數(shù)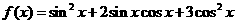 ,
,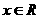 .求:
.求:
(I) 函數(shù)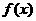 的最大值及取得最大值的自變量
的最大值及取得最大值的自變量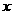 的集合;
的集合;
(II) 函數(shù)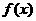 的單調(diào)增區(qū)間.
的單調(diào)增區(qū)間.
(18) (本小題滿分12分)]
已知正方形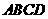 .
.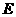 、
、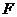 分別是
分別是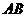 、
、 的中點(diǎn),將
的中點(diǎn),將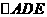 沿
沿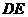 折起,如圖所示,記二面角
折起,如圖所示,記二面角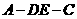 的大小為
的大小為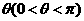 .
.
(I) 證明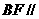 平面
平面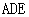 ;
;
(II)若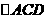 為正三角形,試判斷點(diǎn)
為正三角形,試判斷點(diǎn) 在平面
在平面 內(nèi)的射影
內(nèi)的射影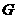 是否在直線
是否在直線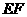 上,證明你的結(jié)論,并求角
上,證明你的結(jié)論,并求角 的余弦值.
的余弦值.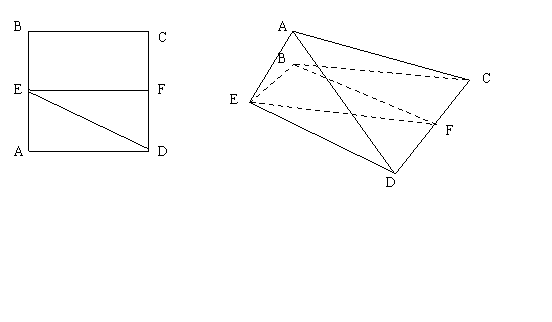

(19) (本小題滿分12分)
現(xiàn)有甲、乙兩個(gè)項(xiàng)目,對(duì)甲項(xiàng)目每投資十萬(wàn)元,一年后利潤(rùn)是1.2萬(wàn)元、1.18萬(wàn)元、1.17萬(wàn)元的概率分別為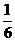 、
、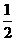 、
、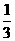 ;已知乙項(xiàng)目的利潤(rùn)與產(chǎn)品價(jià)格的調(diào)整有關(guān),在每次調(diào)整中價(jià)格下降的概率都是
;已知乙項(xiàng)目的利潤(rùn)與產(chǎn)品價(jià)格的調(diào)整有關(guān),在每次調(diào)整中價(jià)格下降的概率都是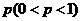 ,設(shè)乙項(xiàng)目產(chǎn)品價(jià)格在一年內(nèi)進(jìn)行2次獨(dú)立的調(diào)整,記乙項(xiàng)目產(chǎn)品價(jià)格在一年內(nèi)的下降次數(shù)為
,設(shè)乙項(xiàng)目產(chǎn)品價(jià)格在一年內(nèi)進(jìn)行2次獨(dú)立的調(diào)整,記乙項(xiàng)目產(chǎn)品價(jià)格在一年內(nèi)的下降次數(shù)為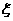 ,對(duì)乙項(xiàng)目每投資十萬(wàn)元,
,對(duì)乙項(xiàng)目每投資十萬(wàn)元, 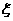 取0、1、2時(shí),
一年后相應(yīng)利潤(rùn)是1.3萬(wàn)元、1.25萬(wàn)元、0.2萬(wàn)元.隨機(jī)變量
取0、1、2時(shí),
一年后相應(yīng)利潤(rùn)是1.3萬(wàn)元、1.25萬(wàn)元、0.2萬(wàn)元.隨機(jī)變量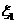 、
、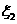 分別表示對(duì)甲、乙兩項(xiàng)目各投資十萬(wàn)元一年后的利潤(rùn).
分別表示對(duì)甲、乙兩項(xiàng)目各投資十萬(wàn)元一年后的利潤(rùn).
(I) 求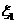 、
、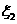 的概率分布和數(shù)學(xué)期望
的概率分布和數(shù)學(xué)期望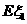 、
、 ;
;
(II) 當(dāng) 時(shí),求
時(shí),求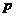 的取值范圍.
的取值范圍.
(20) (本小題滿分14分)
已知點(diǎn)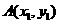 ,
,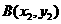
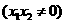 是拋物線
是拋物線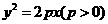 上的兩個(gè)動(dòng)點(diǎn),
上的兩個(gè)動(dòng)點(diǎn), 是坐標(biāo)原點(diǎn),向量
是坐標(biāo)原點(diǎn),向量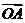 ,
, 滿足
滿足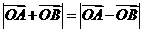 .設(shè)圓
.設(shè)圓 的方程為
的方程為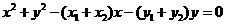
(I) 證明線段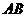 是圓
是圓 的直徑;
的直徑;
(II)當(dāng)圓C的圓心到直線X-2Y=0的距離的最小值為時(shí),求P的值。
21.(本小題滿分12分)
已知函數(shù)f(x)= ,其中a , b , c是以d為公差的等差數(shù)列,,且a>0,d>0.設(shè)
,其中a , b , c是以d為公差的等差數(shù)列,,且a>0,d>0.設(shè)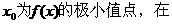 [1-
[1-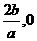 ]上,
]上,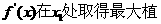 ,在
,在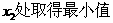 ,將點(diǎn)
,將點(diǎn)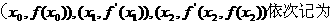 A, B, C
A, B, C
(I)求
(II)若⊿ABC有一邊平行于x軸,且面積為 ,求a ,d的值
,求a ,d的值
(13) 設(shè)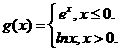 則
則 __________
__________
(14) 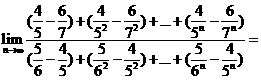 _____________
_____________
(15) 5名乒乓球隊(duì)員中,有2名老隊(duì)員和3名新隊(duì)員.現(xiàn)從中選出3名隊(duì)員排成1、2、3號(hào)參加團(tuán)體比賽,則入選的3名隊(duì)員中至少有一名老隊(duì)員,且1、2號(hào)中至少有1名新隊(duì)員的排法有_______種.(以數(shù)作答)
(16) 若一條直線與一個(gè)正四棱柱各個(gè)面所成的角都為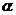 ,則
,則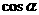 =______
=______
(1)
設(shè)集合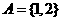 ,則滿足
,則滿足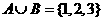 的集合B的個(gè)數(shù)是
的集合B的個(gè)數(shù)是
(A)1 (B)3 (C)4 (D)8
(2) 設(shè)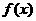 是R上的任意函數(shù),則下列敘述正確的是
是R上的任意函數(shù),則下列敘述正確的是
(A) 是奇函數(shù) (B)
是奇函數(shù) (B)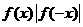 是奇函數(shù)
是奇函數(shù)
(C) 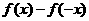 是偶函數(shù) (D)
是偶函數(shù) (D)  是偶函數(shù)
是偶函數(shù)
(3) 給出下列四個(gè)命題:
①垂直于同一直線的兩條直線互相平行.
②垂直于同一平面的兩個(gè)平面互相平行.
③若直線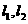 與同一平面所成的角相等,則
與同一平面所成的角相等,則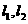 互相平行.
互相平行.
④若直線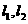 是異面直線,則與
是異面直線,則與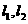 都相交的兩條直線是異面直線.
都相交的兩條直線是異面直線.
其中假命題的個(gè)數(shù)是
(A)1 (B)2 (C)3 (D)4
(4) 雙曲線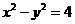 的兩條漸近線與直線
的兩條漸近線與直線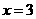 圍成一個(gè)三角形區(qū)域,表示該區(qū)域的不等式組是
圍成一個(gè)三角形區(qū)域,表示該區(qū)域的不等式組是
(A)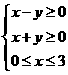 (B)
(B)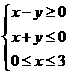 (C)
(C)  (D)
(D) 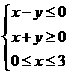
(5) 設(shè)+是R上的一個(gè)運(yùn)算,A是R的非空子集,若對(duì)任意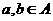 有
有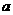 +
+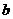
 ,則稱A對(duì)運(yùn)算+封閉,下列數(shù)集對(duì)加法、減法、乘法和除法(除數(shù)不等于零)四則運(yùn)算都封閉的是
,則稱A對(duì)運(yùn)算+封閉,下列數(shù)集對(duì)加法、減法、乘法和除法(除數(shù)不等于零)四則運(yùn)算都封閉的是
(A)自然數(shù)集 (B)整數(shù)集 (C)有理數(shù)集 (D)無(wú)理數(shù)集
(6)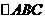 的三內(nèi)角
的三內(nèi)角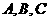 所對(duì)邊的長(zhǎng)分別為
所對(duì)邊的長(zhǎng)分別為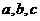 設(shè)向量
設(shè)向量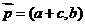 ,
,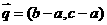 ,若
,若 ,則角
,則角 的大小為
的大小為
(A)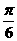 (B)
(B)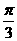 (C)
(C) 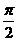 (D)
(D) 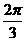
(7) 與方程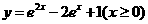 的曲線關(guān)于直線
的曲線關(guān)于直線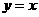 對(duì)稱的曲線的方程為
對(duì)稱的曲線的方程為
(A) (B)
(B) 
(C) 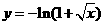 (D)
(D) 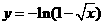
(8) 曲線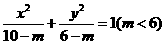 與曲線
與曲線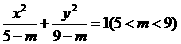 的
的
(A)焦距相等 (B) 離心率相等 (C)焦點(diǎn)相同 (D)準(zhǔn)線相同
(9) 在等比數(shù)列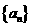 中,
中, ,前
,前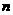 項(xiàng)和為
項(xiàng)和為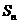 ,若數(shù)列
,若數(shù)列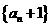 也是等比數(shù)列,則
也是等比數(shù)列,則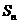 等于
等于
(A)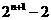 (B)
(B) 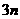 (C)
(C)  (D)
(D)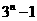
(10) 直線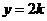 與曲線
與曲線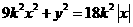
 的公共點(diǎn)的個(gè)數(shù)為
的公共點(diǎn)的個(gè)數(shù)為
(A)1 (B)2 (C)3 (D)4
(11)已知函數(shù)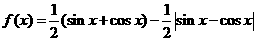 ,則
,則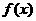 的值域是
的值域是
(A)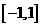 (B)
(B) 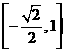 (C)
(C) 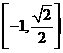 (D)
(D) 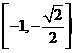
(12) 設(shè) ,
,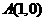 ,
, ,點(diǎn)
,點(diǎn)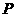 是線段
是線段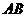 上的一個(gè)動(dòng)點(diǎn),
上的一個(gè)動(dòng)點(diǎn),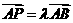 ,若
,若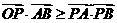 ,則實(shí)數(shù)
,則實(shí)數(shù)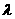 的取值范圍是
的取值范圍是
(A)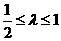 (B)
(B) 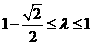 (C)
(C)  (D)
(D) 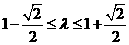
22.(本小題滿分12分)
已知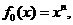
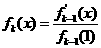 ,其中
,其中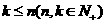 ,
,
設(shè)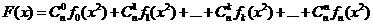 ,
,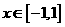 .
.
(I) 寫出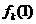 ;
;
(II) 證明:對(duì)任意的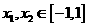 ,恒有
,恒有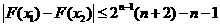 .
.
[解析](I)由已知推得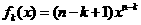 ,從而有
,從而有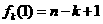
(II) 證法1:當(dāng) 時(shí),
時(shí),
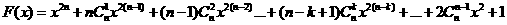
當(dāng)x>0時(shí), 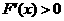 ,所以
,所以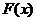 在[0,1]上為增函數(shù)
在[0,1]上為增函數(shù)
因函數(shù)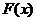 為偶函數(shù)所以
為偶函數(shù)所以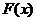 在[-1,0]上為減函數(shù)
在[-1,0]上為減函數(shù)
所以對(duì)任意的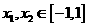
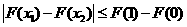
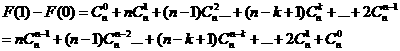
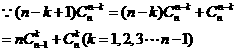
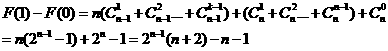
因此結(jié)論成立.
證法2: 當(dāng) 時(shí),
時(shí),
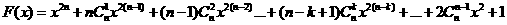
當(dāng)x>0時(shí), 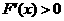 ,所以
,所以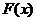 在[0,1]上為增函數(shù)
在[0,1]上為增函數(shù)
因函數(shù)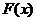 為偶函數(shù)所以
為偶函數(shù)所以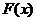 在[-1,0]上為減函數(shù)
在[-1,0]上為減函數(shù)
所以對(duì)任意的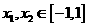
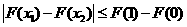
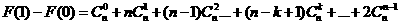
又因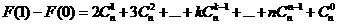
所以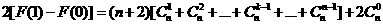
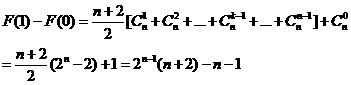
因此結(jié)論成立.
證法3: 當(dāng) 時(shí),
時(shí),
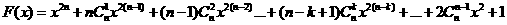
當(dāng)x>0時(shí), 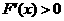 ,所以
,所以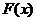 在[0,1]上為增函數(shù)
在[0,1]上為增函數(shù)
因函數(shù)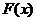 為偶函數(shù)所以
為偶函數(shù)所以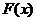 在[-1,0]上為減函數(shù)
在[-1,0]上為減函數(shù)
所以對(duì)任意的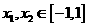
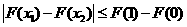
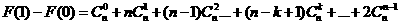
由
對(duì)上式兩邊求導(dǎo)得

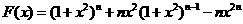
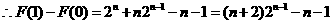
因此結(jié)論成立.
[點(diǎn)評(píng)]本小題考查導(dǎo)數(shù)的基本計(jì)算,函數(shù)的性質(zhì),絕對(duì)值不等式及組合數(shù)性質(zhì)等基礎(chǔ)知識(shí),考查歸納推理能力以及綜合運(yùn)用數(shù)學(xué)知識(shí)分析問(wèn)題和解決問(wèn)題的能力.
(17) (本小題滿分12分)
已知函數(shù)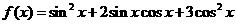 ,
,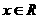 .求:
.求:
(I) 函數(shù)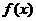 的最大值及取得最大值的自變量
的最大值及取得最大值的自變量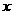 的集合;
的集合;
(II) 函數(shù)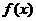 的單調(diào)增區(qū)間.
的單調(diào)增區(qū)間.
[解析](I) 解法一:
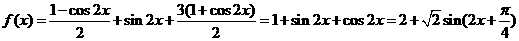
 當(dāng)
當(dāng)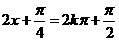 ,即
,即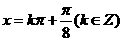 時(shí),
時(shí), 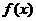 取得最大值
取得最大值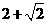 .
.
函數(shù)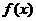 的取得最大值的自變量
的取得最大值的自變量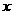 的集合為
的集合為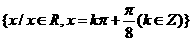 .
.
解法二:

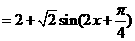
 當(dāng)
當(dāng)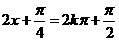 ,即
,即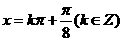 時(shí),
時(shí), 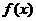 取得最大值
取得最大值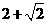 .
.
函數(shù)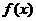 的取得最大值的自變量
的取得最大值的自變量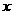 的集合為
的集合為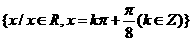 .
.
(II)解:

由題意得: 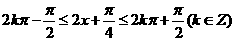
即: 
因此函數(shù)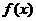 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為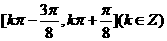 .
.
[點(diǎn)評(píng)]本小題考查三角公式,三角函數(shù)的性質(zhì)及已知三角函數(shù)值求角等基礎(chǔ)知識(shí),考查綜合運(yùn)用三角有關(guān)知識(shí)的能力.
(18) (本小題滿分12分)]
已知正方形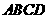 .
. 、
、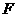 分別是
分別是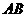 、
、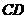 的中點(diǎn),將
的中點(diǎn),將 沿
沿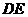 折起,如圖所示,記二面角
折起,如圖所示,記二面角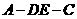 的大小為
的大小為 .
.
(I) 證明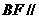 平面
平面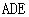 ;
;
(II)若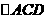 為正三角形,試判斷點(diǎn)
為正三角形,試判斷點(diǎn) 在平面
在平面 內(nèi)的射影
內(nèi)的射影 是否在直線
是否在直線 上,證明你的結(jié)論,并求角
上,證明你的結(jié)論,并求角 的余弦值.
的余弦值.
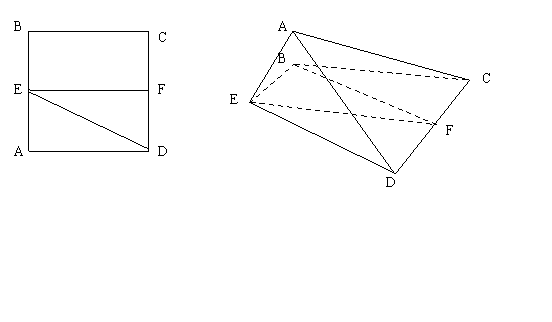

[解析](I)證明:EF分別為正方形ABCD得邊AB、CD的中點(diǎn),
 EB//FD,且EB=FD,
EB//FD,且EB=FD,
 四邊形EBFD為平行四邊形.
四邊形EBFD為平行四邊形.
 BF//ED
BF//ED

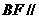 平面
平面 .
.
(II)解法1:
如右圖,點(diǎn)A在平面BCDE內(nèi)的射影G在直線EF上,
過(guò)點(diǎn)A作AG垂直于平面BCDE,垂足為G,連結(jié)GC,GD.

 ACD為正三角形,
ACD為正三角形,
 AC=AD
AC=AD
 CG=GD
CG=GD
 G在CD的垂直平分線上,
G在CD的垂直平分線上,
 點(diǎn)A在平面BCDE內(nèi)的射影G在直線EF上,
點(diǎn)A在平面BCDE內(nèi)的射影G在直線EF上,
過(guò)G作GH垂直于ED于H,連結(jié)AH,則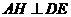 ,所以
,所以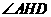 為二面角A-DE-C的平面角.即
為二面角A-DE-C的平面角.即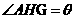
設(shè)原正方體的邊長(zhǎng)為2a,連結(jié)AF
在折后圖的 AEF中,AF=
AEF中,AF=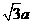 ,EF=2AE=2a,
,EF=2AE=2a,
即 AEF為直角三角形,
AEF為直角三角形, 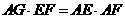

在Rt ADE中,
ADE中, 
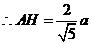
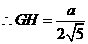
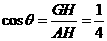 .
.
解法2:點(diǎn)A在平面BCDE內(nèi)的射影G在直線EF上
連結(jié)AF,在平面AEF內(nèi)過(guò)點(diǎn)作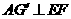 ,垂足為
,垂足為 .
.

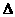 ACD為正三角形,F為CD的中點(diǎn),
ACD為正三角形,F為CD的中點(diǎn),
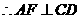
又因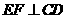 ,
,
所以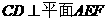
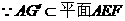
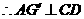
又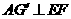 且
且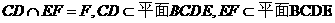
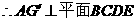
 為A在平面BCDE內(nèi)的射影G.
為A在平面BCDE內(nèi)的射影G.
即點(diǎn)A在平面BCDE內(nèi)的射影在直線EF上
過(guò)G作GH垂直于ED于H,連結(jié)AH,則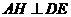 ,所以
,所以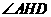 為二面角A-DE-C的平面角.即
為二面角A-DE-C的平面角.即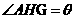
設(shè)原正方體的邊長(zhǎng)為2a,連結(jié)AF
在折后圖的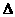 AEF中,AF=
AEF中,AF=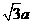 ,EF=2AE=2a,
,EF=2AE=2a,
即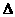 AEF為直角三角形,
AEF為直角三角形, 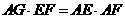

在Rt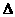 ADE中,
ADE中, 
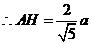
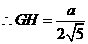
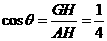 .
.
解法3: 點(diǎn)A在平面BCDE內(nèi)的射影G在直線EF上
連結(jié)AF,在平面AEF內(nèi)過(guò)點(diǎn)作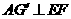 ,垂足為
,垂足為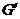 .
.

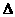 ACD為正三角形,F為CD的中點(diǎn),
ACD為正三角形,F為CD的中點(diǎn),
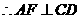
又因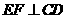 ,
,
所以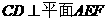
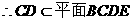
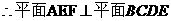
又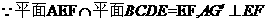
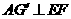
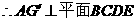
 為A在平面BCDE內(nèi)的射影G.
為A在平面BCDE內(nèi)的射影G.
即點(diǎn)A在平面BCDE內(nèi)的射影在直線EF上
過(guò)G作GH垂直于ED于H,連結(jié)AH,則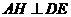 ,所以
,所以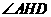 為二面角A-DE-C的平面角.即
為二面角A-DE-C的平面角.即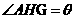
設(shè)原正方體的邊長(zhǎng)為2a,連結(jié)AF
在折后圖的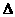 AEF中,AF=
AEF中,AF=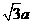 ,EF=2AE=2a,
,EF=2AE=2a,
即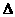 AEF為直角三角形,
AEF為直角三角形, 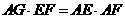

在Rt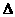 ADE中,
ADE中, 
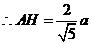
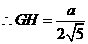 ,
,
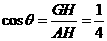 .
.
[點(diǎn)評(píng)]本小題考查空間中的線面關(guān)系,解三角形等基礎(chǔ)知識(shí)考查空間想象能力和思維能力.
(19) (本小題滿分12分)
現(xiàn)有甲、乙兩個(gè)項(xiàng)目,對(duì)甲項(xiàng)目每投資十萬(wàn)元,一年后利潤(rùn)是1.2萬(wàn)元、1.18萬(wàn)元、1.17萬(wàn)元的概率分別為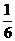 、
、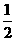 、
、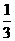 ;已知乙項(xiàng)目的利潤(rùn)與產(chǎn)品價(jià)格的調(diào)整有關(guān),在每次調(diào)整中價(jià)格下降的概率都是
;已知乙項(xiàng)目的利潤(rùn)與產(chǎn)品價(jià)格的調(diào)整有關(guān),在每次調(diào)整中價(jià)格下降的概率都是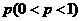 ,設(shè)乙項(xiàng)目產(chǎn)品價(jià)格在一年內(nèi)進(jìn)行2次獨(dú)立的調(diào)整,記乙項(xiàng)目產(chǎn)品價(jià)格在一年內(nèi)的下降次數(shù)為
,設(shè)乙項(xiàng)目產(chǎn)品價(jià)格在一年內(nèi)進(jìn)行2次獨(dú)立的調(diào)整,記乙項(xiàng)目產(chǎn)品價(jià)格在一年內(nèi)的下降次數(shù)為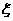 ,對(duì)乙項(xiàng)目每投資十萬(wàn)元,
,對(duì)乙項(xiàng)目每投資十萬(wàn)元, 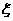 取0、1、2時(shí),
一年后相應(yīng)利潤(rùn)是1.3萬(wàn)元、1.25萬(wàn)元、0.2萬(wàn)元.隨機(jī)變量
取0、1、2時(shí),
一年后相應(yīng)利潤(rùn)是1.3萬(wàn)元、1.25萬(wàn)元、0.2萬(wàn)元.隨機(jī)變量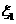 、
、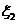 分別表示對(duì)甲、乙兩項(xiàng)目各投資十萬(wàn)元一年后的利潤(rùn).
分別表示對(duì)甲、乙兩項(xiàng)目各投資十萬(wàn)元一年后的利潤(rùn).
(I) 求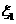 、
、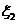 的概率分布和數(shù)學(xué)期望
的概率分布和數(shù)學(xué)期望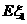 、
、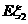 ;
;
(II) 當(dāng)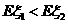 時(shí),求
時(shí),求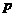 的取值范圍.
的取值范圍.
[解析]
(I)解法1:
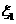 的概率分布為
的概率分布為
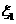 |
1.2 |
1.18 |
1.17 |
|
P |
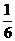 |
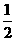 |
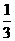 |
E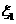 =1.2
=1.2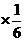 +1.18
+1.18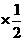 +1.17
+1.17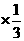 =1.18.
=1.18.
由題設(shè)得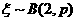 ,則
,則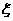 的概率分布為
的概率分布為
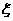 |
0 |
1 |
2 |
|
P |
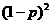 |
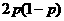 |
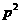 |
故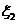 的概率分布為
的概率分布為
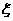 |
1.3 |
1.25 |
0.2 |
|
P |
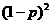 |
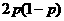 |
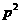 |
所以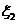 的數(shù)學(xué)期望為
的數(shù)學(xué)期望為
E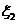 =
=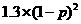 +
+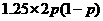 +
+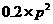 =
=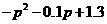 .
.
解法2: 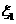 的概率分布為
的概率分布為
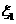 |
1.2 |
1.18 |
1.17 |
|
P |
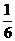 |
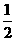 |
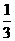 |
E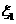 =1.2
=1.2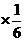 +1.18
+1.18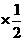 +1.17
+1.17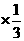 =1.18.
=1.18.
設(shè) 表示事件”第i次調(diào)整,價(jià)格下降”(i=1,2),則
表示事件”第i次調(diào)整,價(jià)格下降”(i=1,2),則
P(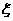 =0)=
=0)= 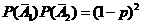 ;
;
P(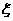 =1)=
=1)=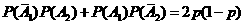 ;
;
P(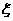 =2)=
=2)=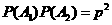
故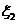 的概率分布為
的概率分布為
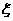 |
1.3 |
1.25 |
0.2 |
|
P |
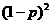 |
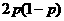 |
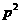 |
所以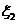 的數(shù)學(xué)期望為
的數(shù)學(xué)期望為
E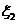 =
=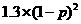 +
+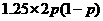 +
+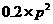 =
=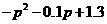 .
.
(II) 由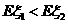 ,得:
,得:
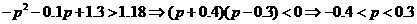
因0<p<1,所以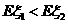 時(shí),p的取值范圍是0<p<0.3.
時(shí),p的取值范圍是0<p<0.3.
[點(diǎn)評(píng)]本小題考查二項(xiàng)分布、分布列、數(shù)學(xué)期望、方差等基礎(chǔ)知識(shí),考查同學(xué)們運(yùn)用概率知識(shí)解決實(shí)際問(wèn)題的能力.
(20) (本小題滿分14分)
已知點(diǎn)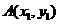 ,
,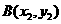
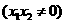 是拋物線
是拋物線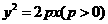 上的兩個(gè)動(dòng)點(diǎn),
上的兩個(gè)動(dòng)點(diǎn), 是坐標(biāo)原點(diǎn),向量
是坐標(biāo)原點(diǎn),向量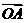 ,
,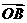 滿足
滿足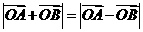 .設(shè)圓
.設(shè)圓 的方程為
的方程為
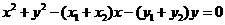
(I) 證明線段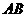 是圓
是圓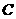 的直徑;
的直徑;
(II)當(dāng)圓C的圓心到直線X-2Y=0的距離的最小值為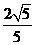 時(shí),求p的值。
時(shí),求p的值。
[解析](I)證明1:
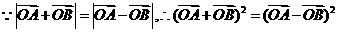
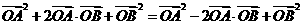
整理得: 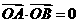
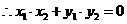
設(shè)M(x,y)是以線段AB為直徑的圓上的任意一點(diǎn),則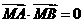
即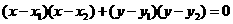
整理得: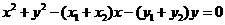
故線段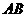 是圓
是圓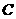 的直徑
的直徑
證明2: 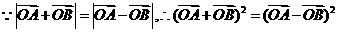
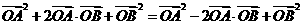
整理得: 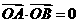
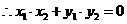 ……..(1)
……..(1)
設(shè)(x,y)是以線段AB為直徑的圓上則
即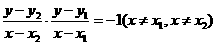
去分母得: 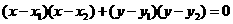
點(diǎn)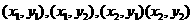 滿足上方程,展開并將(1)代入得:
滿足上方程,展開并將(1)代入得:
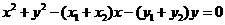
故線段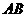 是圓
是圓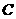 的直徑
的直徑
證明3: 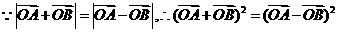
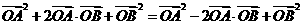
整理得: 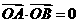
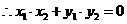 ……(1)
……(1)
以線段AB為直徑的圓的方程為
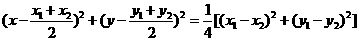
展開并將(1)代入得:
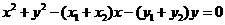
故線段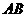 是圓
是圓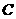 的直徑
的直徑
(II)解法1:設(shè)圓C的圓心為C(x,y),則
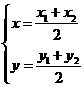
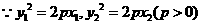
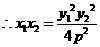
又因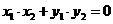
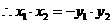
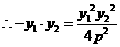
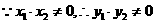
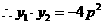
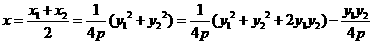
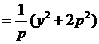
所以圓心的軌跡方程為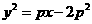
設(shè)圓心C到直線x-2y=0的距離為d,則
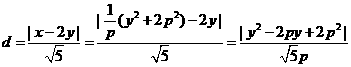
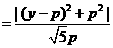
當(dāng)y=p時(shí),d有最小值 ,由題設(shè)得
,由題設(shè)得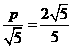
 .
.
解法2: 設(shè)圓C的圓心為C(x,y),則
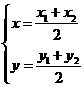
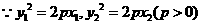
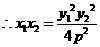
又因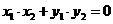
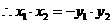
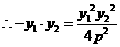
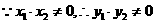
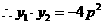
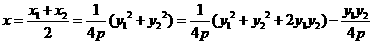
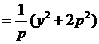
所以圓心的軌跡方程為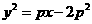
設(shè)直線x-2y+m=0到直線x-2y=0的距離為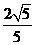 ,則
,則
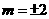
因?yàn)閤-2y+2=0與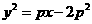 無(wú)公共點(diǎn),
無(wú)公共點(diǎn),
所以當(dāng)x-2y-2=0與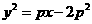 僅有一個(gè)公共點(diǎn)時(shí),該點(diǎn)到直線x-2y=0的距離最小值為
僅有一個(gè)公共點(diǎn)時(shí),該點(diǎn)到直線x-2y=0的距離最小值為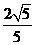

將(2)代入(3)得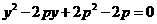
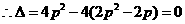

解法3: 設(shè)圓C的圓心為C(x,y),則
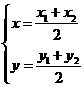
圓心C到直線x-2y=0的距離為d,則
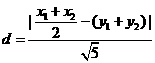
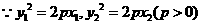
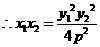
又因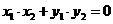
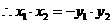
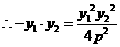
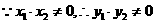
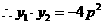
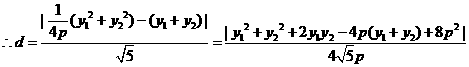
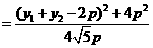
當(dāng)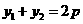 時(shí),d有最小值
時(shí),d有最小值 ,由題設(shè)得
,由題設(shè)得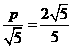
 .
.
[點(diǎn)評(píng)]本小題考查了平面向量的基本運(yùn)算,圓與拋物線的方程.點(diǎn)到直線的距離公式等基礎(chǔ)知識(shí),以及綜合運(yùn)用解析幾何知識(shí)解決問(wèn)題的能力.
21.(本小題滿分12分)
已知函數(shù)f(x)=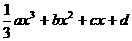 ,其中a , b , c是以d為公差的等差數(shù)列,,且a>0,d>0.設(shè)
,其中a , b , c是以d為公差的等差數(shù)列,,且a>0,d>0.設(shè)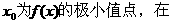 [1-
[1-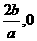 ]上,
]上,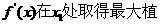 ,在
,在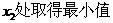 ,將點(diǎn)
,將點(diǎn)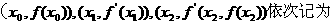 A, B, C
A, B, C
(I)求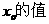
(II)若⊿ABC有一邊平行于x軸,且面積為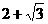 ,求a ,d的值
,求a ,d的值
[解析](I)解:
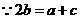
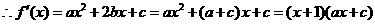
令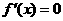 ,得
,得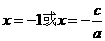

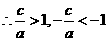
當(dāng)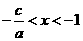 時(shí),
時(shí), 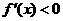 ;
;
當(dāng)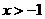 時(shí),
時(shí), 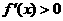
所以f(x)在x=-1處取得最小值即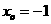
(II) 
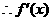 的圖像的開口向上,對(duì)稱軸方程為
的圖像的開口向上,對(duì)稱軸方程為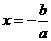
由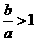 知
知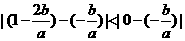
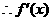 在
在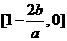 上的最大值為
上的最大值為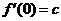
即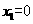
又由
 當(dāng)
當(dāng)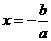 時(shí),
時(shí), 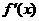 取得最小值為
取得最小值為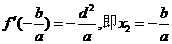

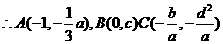
由三角形ABC有一條邊平行于x軸知AC平行于x軸,所以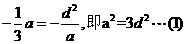
又由三角形ABC的面積為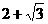 得
得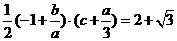
利用b=a+d,c=a+2d,得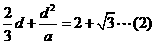
聯(lián)立(1)(2)可得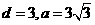 .
.
解法2: 

又c>0知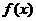 在
在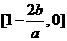 上的最大值為
上的最大值為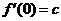
即: 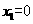
又由
 當(dāng)
當(dāng)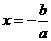 時(shí),
時(shí), 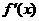 取得最小值為
取得最小值為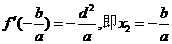

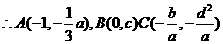
由三角形ABC有一條邊平行于x軸知AC平行于x軸,所以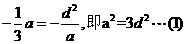
又由三角形ABC的面積為 得
得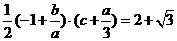
利用b=a+d,c=a+2d,得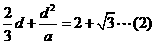
聯(lián)立(1)(2)可得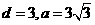
[點(diǎn)評(píng)]本小題考查了函數(shù)的導(dǎo)數(shù),函數(shù)的極值的判定,閉區(qū)間上二次函數(shù)的最值,等差數(shù)基礎(chǔ)知識(shí)的綜合應(yīng)用,考查了應(yīng)用數(shù)形結(jié)合的數(shù)學(xué)思想分析問(wèn)題解決問(wèn)題的能力
(13) 設(shè)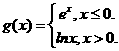 則
則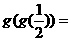 __________
__________
[解析]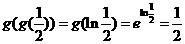 .
.
[點(diǎn)評(píng)]本題考察了分段函數(shù)的表達(dá)式、指對(duì)數(shù)的運(yùn)算.
(14)  _____________
_____________
[解析]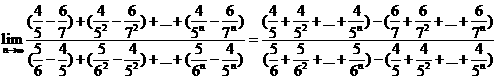
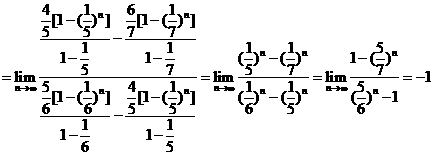
[點(diǎn)評(píng)]本題考查了等比數(shù)列的求和公式以及數(shù)列極限的基本類型.
(15) 5名乒乓球隊(duì)員中,有2名老隊(duì)員和3名新隊(duì)員.現(xiàn)從中選出3名隊(duì)員排成1、2、3號(hào)參加團(tuán)體比賽,則入選的3名隊(duì)員中至少有一名老隊(duì)員,且1、2號(hào)中至少有1名新隊(duì)員的排法有_______種.(以數(shù)作答)
[解析]兩老一新時(shí), 有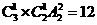 種排法;
種排法;
兩新一老時(shí), 有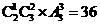 種排法,即共有48種排法.
種排法,即共有48種排法.
[點(diǎn)評(píng)]本題考查了有限制條件的排列組合問(wèn)題以及分類討論思想.
(16) 若一條直線與一個(gè)正四棱柱各個(gè)面所成的角都為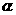 ,則
,則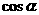 =______
=______
[解析]不妨認(rèn)為一個(gè)正四棱柱為正方體,與正方體的所有面成角相等時(shí),為與相交于同一頂點(diǎn)的三個(gè)相互垂直的平面所成角相等,即為體對(duì)角線與該正方體所成角.故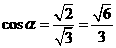 .
.
[點(diǎn)評(píng)]本題考查了直線與平面所成角的定義以及正四棱柱的概念,充分考查了轉(zhuǎn)化思想的應(yīng)用.
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com