
已知 均為正數,證明:
均為正數,證明: ,并確定
,并確定 為何值時,等號成立。
為何值時,等號成立。
利用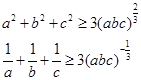 ①所以
①所以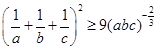 ② ……6分
② ……6分
故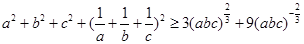 .
.
又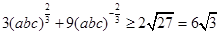 ③
③
(證法二)利用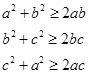 證明。
證明。
解析試題分析:(證法一)因為a,b,c均為正數,由平均值不等式得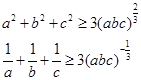 ①所以
①所以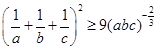 ② ……6分
② ……6分
故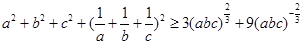 .
.
又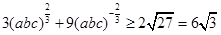 ③
③
所以原不等式成立. ……8分
當且僅當a=b=c時,①式和②式等號成立。當且僅當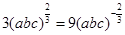 時,③式等號成立。即當且僅當a=b=c=
時,③式等號成立。即當且僅當a=b=c=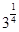 時,原式等號成立。 ……10分
時,原式等號成立。 ……10分
(證法二)因為a,b,c均為正數,由基本不等式得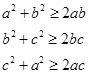
所以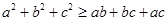 ①
①
同理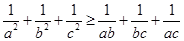 ② ……6分
② ……6分
故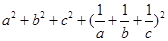
 ③
③
所以原不等式成立. ……8分
當且僅當a=b=c時,①式和②式等號成立,當且僅當a=b=c,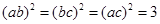 時,③式等號成立。
時,③式等號成立。
即當且僅當a=b=c=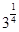 時,原式等號成立。 ……10分
時,原式等號成立。 ……10分
考點:本題主要考查簡單不等式的證明。
點評:中檔題,不等式的證明方法,通常有“綜合法”、“分析法”“反證法”等,不等式的性質、基本不等式等基礎知識,是不等式證明的基礎,應牢記并靈活運用。本題證法較多,入口較易。


 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com