
| PM2.5日均值m(微克/立方米) | 空氣質量等級 |
 | 一級 |
 | 二級 |
 | 超標 |

 表示空氣質量達到一級的天數,求
表示空氣質量達到一級的天數,求 的分布列;
的分布列; 計算每種情況的概率,再列出分布列;第三問,在10天中,
計算每種情況的概率,再列出分布列;第三問,在10天中, 的有4天,所以每天空氣質量達到一級的概率為
的有4天,所以每天空氣質量達到一級的概率為 ,利用二項分布,利用
,利用二項分布,利用 直接計算數學期望.
直接計算數學期望. ,
, 的可能值為0,1,2,3
的可能值為0,1,2,3 
 即得分布列:
即得分布列: | 0 | 1 | 2 | 3 |
 |  |  |  | 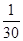 |
 ,由
,由 ~
~ , 得到
, 得到 (天) ,
(天) ,

科目:高中數學 來源:不詳 題型:解答題
 型血的人數占總人口數的比為
型血的人數占總人口數的比為 ,現從中隨機抽取3人.
,現從中隨機抽取3人.  型血的概率;
型血的概率; 型血的人數為
型血的人數為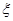 ,求
,求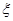 的概率分布與數學期望.
的概率分布與數學期望.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
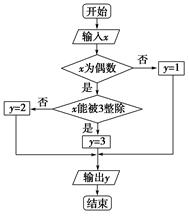
| 運行次數n | 輸出y的值 為1的頻數 | 輸出y的值 為2的頻數 | 輸出y的值 為3的頻數 |
| 30 | 14 | 6 | 10 |
| … | … | … | … |
| 2 100 | 1 027 | 376 | 697 |
| 運行次數n | 輸出y的值 為1的頻數 | 輸出y的值 為2的頻數 | 輸出y的值 為3的頻數 |
| 30 | 12 | 11 | 7 |
| … | … | … | … |
| 2 100 | 1 051 | 696 | 353 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com