
已知數列 的前
的前 項和為
項和為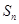 ,數列
,數列 是公比為
是公比為 的等比數列,
的等比數列, 是
是 和
和 的等比中項.
的等比中項.
(1)求數列 的通項公式;
的通項公式;
(2)求數列 的前
的前 項和
項和 .
.
(1)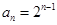 ;(2)
;(2) .
.
解析試題分析:(1)數列中可根據通項 的特點選擇對應的方法來求
的特點選擇對應的方法來求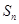 ,反之也可根據
,反之也可根據 ,利用
,利用 來再求
來再求 ,此題可先根據條件求出
,此題可先根據條件求出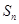 ,然后就不難求
,然后就不難求 了;(2)由(1)不難得到數列
了;(2)由(1)不難得到數列 通項公式,根據通項公式的特點應選擇用錯位相減法來求數列前
通項公式,根據通項公式的特點應選擇用錯位相減法來求數列前 項和
項和 .特殊數列的求和方法通常有:①公式法;②分解法;③拆項相消法;④錯位相減法;⑤奇偶分析法;⑥倒序相加法等等,關鍵是掌握根據通項所具有的特點來選擇對應的求和方法,這份試卷中已經考查了兩種特殊數列求和方法——拆項相消法和錯位相減法,通常一個等差數列和一個等比數列對應項相乘得到的數列求前
.特殊數列的求和方法通常有:①公式法;②分解法;③拆項相消法;④錯位相減法;⑤奇偶分析法;⑥倒序相加法等等,關鍵是掌握根據通項所具有的特點來選擇對應的求和方法,這份試卷中已經考查了兩種特殊數列求和方法——拆項相消法和錯位相減法,通常一個等差數列和一個等比數列對應項相乘得到的數列求前 項的和時常用錯位相減法,這個方法不難掌握,但要把題目做正確還是有一定難度的,故有“人人會做,人人都有可能做不對”一說,所以要特別關注易錯之處.
項的和時常用錯位相減法,這個方法不難掌握,但要把題目做正確還是有一定難度的,故有“人人會做,人人都有可能做不對”一說,所以要特別關注易錯之處.
試題解析:(1)∵ 是公比為
是公比為 的等比數列,∴
的等比數列,∴ ,
,
∴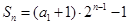 ,從而
,從而 ,
,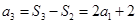 ,
,
∵ 是
是 和
和 的等比中項,∴
的等比中項,∴ ,解得
,解得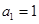 或
或 ,
,
當 時,
時, ,
, 不是等比數列,∴
不是等比數列,∴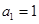 ,∴
,∴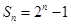 ,
,
當 時,
時,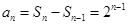 ,∵
,∵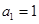 符合
符合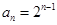 ,∴
,∴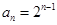 ; (6分)
; (6分)
(2)∵ ,
,
∴ ①
①
① 得:
得: ②
②
① ②得:
②得:
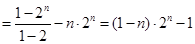 ,
,
∴ . (14分)
. (14分)
考點:1.等比數列通項公式及前 項和公式;2.等比中項;3.特殊數列求和方法之一:錯位相減法.
項和公式;2.等比中項;3.特殊數列求和方法之一:錯位相減法.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
已知各項均為正數的等比數列{an}滿足a3 =8,a5 +a7=160,{an}的前n項和為Sn.
(1)求an;
(2)若數列{bn}的通項公式為bn=(-1)n·n(n∈N+),求數列{an·bn}的前n項和Tn。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com