
已知數列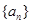 是等差數列,
是等差數列,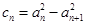 (
( ).
).
(Ⅰ)判斷數列 是否是等差數列,并說明理由;
是否是等差數列,并說明理由;
(Ⅱ)如果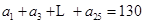 ,
, (
( 為常數),試寫出數列
為常數),試寫出數列 的通項公式;
的通項公式;
(Ⅲ)在(Ⅱ)的條件下,若數列 得前
得前 項和為
項和為 ,問是否存在這樣的實數
,問是否存在這樣的實數 ,使
,使 當且僅當
當且僅當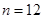 時取得最大值.若存在,求出
時取得最大值.若存在,求出 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
(Ⅰ)數列 是等差數列;(Ⅱ)
是等差數列;(Ⅱ)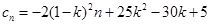 ;(Ⅲ)
;(Ⅲ)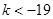 或
或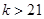 .
.
解析試題分析:(Ⅰ)等差數列的證明一般是從定義出發,注意若用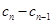 為常數,則需
為常數,則需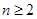 且
且 ;若用若用
;若用若用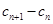 則
則 為常數,則需
為常數,則需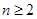 .(Ⅱ)因為
.(Ⅱ)因為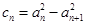 ,所以求數列
,所以求數列 的通項公式,關鍵是先求出等差數列
的通項公式,關鍵是先求出等差數列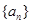 的通項公式,即求出
的通項公式,即求出 ,這樣就必須建立關于
,這樣就必須建立關于 的兩個方程,求出
的兩個方程,求出 ,顯然必須從條件提供的兩個等式出發去求解,注意求解的技巧;(Ⅲ)關于等差數列前
,顯然必須從條件提供的兩個等式出發去求解,注意求解的技巧;(Ⅲ)關于等差數列前 項和的最值問題,通常有兩個思路,其一,從求和公式考慮,因為求和公式是關于
項和的最值問題,通常有兩個思路,其一,從求和公式考慮,因為求和公式是關于 的二次式,可以結合二次函數知識解決問題,但要注意數列自身的特點,即
的二次式,可以結合二次函數知識解決問題,但要注意數列自身的特點,即 ;其二,從通項考慮,看何時變號.此題從通項考慮比較好.
;其二,從通項考慮,看何時變號.此題從通項考慮比較好.
試題解析:(Ⅰ)設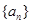 的公差為
的公差為 ,則
,則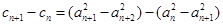

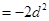
 數列
數列 是以
是以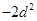 為公差的等差數列.
為公差的等差數列.
(Ⅱ)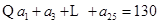

 兩式相減:
兩式相減: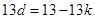
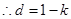
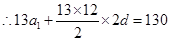 ,
,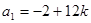
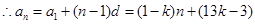

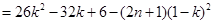
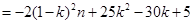
(Ⅲ)因為當且僅當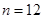 時
時 最大
最大 有
有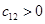 ,
,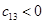 ,
,
即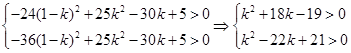
由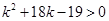 解得
解得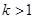 或
或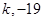 ;由
;由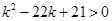 解得
解得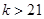 或
或 ,
,
綜合得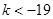 或
或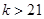 .
.
考點:等差數列的定義及求和、求通項.


 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com