
已知拋物線 :
: 的焦點為
的焦點為 ,若過點
,若過點 且斜率為
且斜率為 的直線與拋物線相交于
的直線與拋物線相交于 兩點,且
兩點,且 .
.
(1)求拋物線 的方程;
的方程;
(2)設直線 為拋物線
為拋物線 的切線,且
的切線,且 ∥
∥ ,
, 為
為 上一點,求
上一點,求 的最小值.
的最小值.
(1) ;(2)-14.
;(2)-14.
解析試題分析:本題主要考查拋物線的標準方程、拋物線的幾何性質、向量的數量積等基礎知識,考查學生的數學結合思想、分析問題解決問題的能力、轉化能力.第一問,由拋物線的標準方程得焦點F的坐標,再利用點斜式寫出直線方程,由于它與拋物線相交,所以直線方程與拋物線方程聯立,消參,利用韋達定理、得到M、N的兩個橫坐標的和,解出P的值,從而得到拋物線的標準方程;第二問,先設出直線 的方程,由于
的方程,由于 是拋物線的切線,所以2個方程聯立,得到x的方程后,方程的判別式等于0,解出b的值,從而得到直線方程,設出p點坐標,結合第一問得出
是拋物線的切線,所以2個方程聯立,得到x的方程后,方程的判別式等于0,解出b的值,從而得到直線方程,設出p點坐標,結合第一問得出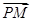 和
和 坐標,利用向量的數量積化簡表達式,使之轉化為關于m的式子,再利用配方法求最值.
坐標,利用向量的數量積化簡表達式,使之轉化為關于m的式子,再利用配方法求最值.
試題解析:(1)由題可知 ,則該直線方程為:
,則該直線方程為: , 1分
, 1分
代入
得: ,設
,設 ,則有
,則有 3分
3分
∵ ,∴
,∴ ,即
,即 ,解得
,解得

∴拋物線的方程為: . 5分
. 5分
(2)設 方程為
方程為 ,代入
,代入 ,得
,得 ,
,
因為 為拋物線
為拋物線 的切線,∴
的切線,∴ ,
,
解得 ,∴
,∴
 7分
7分
由(1)可知: ,
,
設 ,則
,則
所以

 ,
, ,
,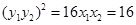 ,
, ,
, ,∴
,∴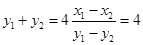
 10分
10分
當且僅當 時,即點
時,即點 的坐標為
的坐標為 時,
時, 的最小值為
的最小值為 . 12分
. 12分
考點:拋物線的標準方程、拋物線的幾何性質、向量的數量積


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
已知向量 ,
, ,
, ,
,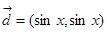 .
.
(1)當 時,求向量
時,求向量 與
與 的夾角
的夾角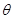 ;
;
(2)當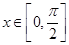 時,求
時,求 的最大值;
的最大值;
(3)設函數 ,將函數
,將函數 的圖像向右平移
的圖像向右平移 個長度單位,向上平移
個長度單位,向上平移 個長度單位
個長度單位 后得到函數
后得到函數 的圖像,且
的圖像,且 ,令
,令 ,求
,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,已知橢圓 的離心率為
的離心率為 ,以橢圓
,以橢圓 的
的
左頂點 為圓心作圓
為圓心作圓 ,設圓
,設圓 與橢圓
與橢圓 交于點
交于點 與點
與點 .
.
(1)求橢圓 的方程;
的方程;
(2)求 的最小值,并求此時圓
的最小值,并求此時圓 的方程;
的方程;
(3)設點 是橢圓
是橢圓 上異于
上異于 、
、 的任意一點,且直線
的任意一點,且直線 、
、 分別與
分別與 軸交于點
軸交于點 、
、 ,
,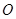 為坐標原點,求證:
為坐標原點,求證: 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知向量a=3e1-2e2,b=4e1+e2,其中e1=(1,0),e2=(0,1),求:
(1)a·b,|a+b|;(2)a與b的夾角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,設 是單位圓上一點,一個動點從點
是單位圓上一點,一個動點從點 出發,沿圓周按逆時針方向勻速旋轉,12秒旋轉一周.
出發,沿圓周按逆時針方向勻速旋轉,12秒旋轉一周. 秒時,動點到達點
秒時,動點到達點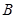 ,
, 秒時動點到達點
秒時動點到達點 .設
.設 ,其縱坐標滿足
,其縱坐標滿足 .
.
(1)求點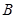 的坐標,并求
的坐標,并求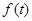 ;
;
(2)若 ,求
,求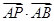 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com