
如圖,已知雙曲線C1: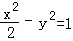 ,曲線C2:|y|=|x|+1,P是平面內一點,若存在過點P的直線與C1,C2都有公共點,則稱P為“C1﹣C2型點“
,曲線C2:|y|=|x|+1,P是平面內一點,若存在過點P的直線與C1,C2都有公共點,則稱P為“C1﹣C2型點“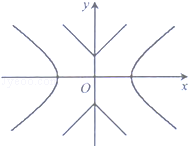
(1)在正確證明C1的左焦點是“C1﹣C2型點“時,要使用一條過該焦點的直線,試寫出一條這樣的直線的方程(不要求驗證);
(2)設直線y=kx與C2有公共點,求證|k|>1,進而證明原點不是“C1﹣C2型點”;
(3)求證:圓x2+y2= 內的點都不是“C1﹣C2型點”
內的點都不是“C1﹣C2型點”
(1)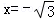 或
或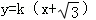 ,其中
,其中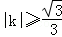 (2)見解析(3)見解析
(2)見解析(3)見解析
解析試題分析:C1的左焦點為(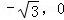 ),寫出的直線方程可以是以下形式:
),寫出的直線方程可以是以下形式: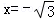 或
或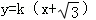 ,其中
,其中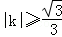 .
.
(2)證明:因為直線y=kx與C2有公共點,
所以方程組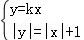 有實數解,因此|kx|=|x|+1,得
有實數解,因此|kx|=|x|+1,得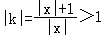 .
.
若原點是“C1﹣C2型點”,則存在過原點的直線與C1、C2都有公共點.
考慮過原點與C2有公共點的直線x=0或y=kx(|k|>1).
顯然直線x=0與C1無公共點.
如果直線為y=kx(|k|>1),則由方程組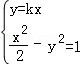 ,得
,得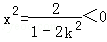 ,矛盾.
,矛盾.
所以直線y=kx(|k|>1)與C1也無公共點.
因此原點不是“C1﹣C2型點”.
(3)證明:記圓O: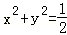 ,取圓O內的一點Q,設有經過Q的直線l與C1,C2都有公共點,顯然l不與x軸垂直,
,取圓O內的一點Q,設有經過Q的直線l與C1,C2都有公共點,顯然l不與x軸垂直,
故可設l:y=kx+b.
若|k|≤1,由于圓O夾在兩組平行線y=x±1與y=﹣x±1之間,因此圓O也夾在直線y=kx±1與y=﹣kx±1之間,
從而過Q且以k為斜率的直線l與C2無公共點,矛盾,所以|k|>1.
因為l與C1由公共點,所以方程組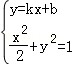 有實數解,
有實數解,
得(1﹣2k2)x2﹣4kbx﹣2b2﹣2=0.
因為|k|>1,所以1﹣2k2≠0,
因此△=(4kb)2﹣4(1﹣2k2)(﹣2b2﹣2)=8(b2+1﹣2k2)≥0,
即b2≥2k2﹣1.
因為圓O的圓心(0,0)到直線l的距離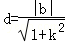 ,
,
所以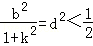 ,從而
,從而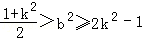 ,得k2<1,與|k|>1矛盾.
,得k2<1,與|k|>1矛盾.
因此,圓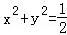 內的點不是“C1﹣C2型點”
內的點不是“C1﹣C2型點”
考點:直線與圓錐曲線的關系;點到直線的距離公式;雙曲線的簡單性質
點評:本題考查了雙曲線的簡單幾何性質,考查了點到直線的距離公式,考查了直線與圓錐曲線的關系,直線與圓錐曲線聯系在一起的綜合題在高考中多以高檔題、壓軸題出現,主要涉及位置關系的判定,弦長問題、最值問題、對稱問題、軌跡問題等.突出考查了數形結合、分類討論、函數與方程、等價轉化等數學思想方法.屬難題


科目:高中數學 來源: 題型:填空題
在平面直角坐標系中,動點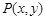 到兩條坐標軸的距離之和等于它到點
到兩條坐標軸的距離之和等于它到點 的距離,記點
的距離,記點 的軌跡為曲線
的軌跡為曲線 .
.
(I) 給出下列三個結論:
①曲線 關于原點對稱;
關于原點對稱;
②曲線 關于直線
關于直線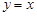 對稱;
對稱;
③曲線 與
與 軸非負半軸,
軸非負半軸,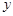 軸非負半軸圍成的封閉圖形的面積小于
軸非負半軸圍成的封閉圖形的面積小于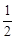 ;
;
其中,所有正確結論的序號是_____;
(Ⅱ)曲線 上的點到原點距離的最小值為______.
上的點到原點距離的最小值為______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com