
已知數列{an},且x= 是函數f(x)=an-1x3-3[(t+1)an-an+1]
x+1(n≥2)的一個極值點.數列{an}中a1=t,a2=t2(t>0且t≠1) .
是函數f(x)=an-1x3-3[(t+1)an-an+1]
x+1(n≥2)的一個極值點.數列{an}中a1=t,a2=t2(t>0且t≠1) .
(1)求數列{an}的通項公式;
(2)記bn=2(1- ),當t=2時,數列{bn}的前n項和為Sn,求使Sn>2010的n的最小值;
),當t=2時,數列{bn}的前n項和為Sn,求使Sn>2010的n的最小值;
(3)若cn= ,證明:
,證明: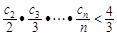 ( n∈N﹡).
( n∈N﹡).
解:(1)f ′(x)=3an-1x2-3[(t+1)an-an+1],
所以f ′(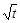 )=3an-1t-3[(t+1)an-an+1]=0.
)=3an-1t-3[(t+1)an-an+1]=0.
整理得:an+1-an=t(an-an-1) .…………………………………………2分
當 t=1時,{an-an-1}是常數列,得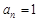 ;
;
當 t≠1時{an-an-1}是以 a2-a1=t2-t為首項, t為公比的等比數列,
所以 an-an-1=(t2-t)·t n-2=(t-1)·t n-1.
方法一:由上式得
(an-an-1)+(an-1-an-2)+…+(a2-a1)=(t-1)(tn-1+tn-2+…+t),
即 an-a1=(t-1)·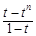 =tn-t,
=tn-t,
所以 an=tn(n≥2) .
又,當t=1時上式仍然成立,故 an=tn(n∈N﹡) .………………………4分
方法二:由上式得: an-tn=an-1-tn-1,
所以{an-tn}是常數列,an-tn=a1-t=0 an=tn(n≥2) .
又,當t=1時上式仍然成立,故 an=tn(n∈N﹡) .
(2)當t=2, bn=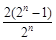 =2-
=2- .
.
∴Sn=2n-(1+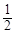 +
+ +…+
+…+ )=2n-
)=2n-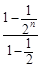
=2n-2(1-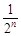 )=2n-2+2·
)=2n-2+2·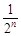
由Sn>2010,得
2n-2+2(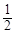 )n>2010, n+(
)n>2010, n+(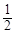 )n>1006,
)n>1006,
當n≤1005時,
n+(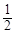 )n<1006,
)n<1006,
當 n≥1006時,
n+(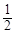 )n>1006,
)n>1006,
因此 n的最小值為1006.………………………………………………8分
(3)cn=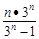 且c1=
且c1=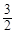 ,所以
,所以
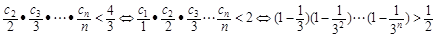 .
.
因為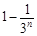 =
= =
=
=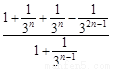 ≥
≥ ,
,
所以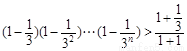
 =
= .
.
從而原命題得證.…………………………………………………………14分
【解析】略


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:高中數學 來源: 題型:
| t |
| 1 |
| an |
| 3nlogtan |
| 3n-1 |
| c2 |
| 2 |
| c3 |
| 3 |
| cn |
| n |
| 4 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| t |
| 3nlogtan |
| 3n- 1 |
| c2 |
| 2 |
| c3 |
| 3 |
| cn |
| n |
| 4 |
| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com