
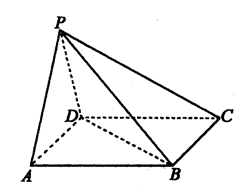
如圖,在四棱錐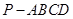 中,底面
中,底面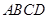 是正方形,側面
是正方形,側面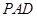 是正三角形,且平面
是正三角形,且平面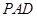 ⊥底面
⊥底面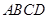
(1)求證: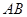 ⊥平面
⊥平面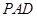
(2)求直線 與底面
與底面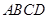 所成角的余弦值;
所成角的余弦值;
(3)設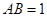 ,求點
,求點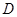 到平面
到平面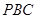 的距離.
的距離.
(1)∵底面ABCD是正方形,∴AB⊥AD,∵平面PAD⊥底面ABCD,AB 底面ABCD,底面ABCD∩平面PAD=AD,∴AB⊥平面PAD;(2)
底面ABCD,底面ABCD∩平面PAD=AD,∴AB⊥平面PAD;(2) ;(3)
;(3)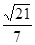
解析試題分析:(1)∵底面ABCD是正方形,∴AB⊥AD,∵平面PAD⊥底面ABCD,AB 底面ABCD,底面ABCD∩平面PAD=AD,∴AB⊥平面PAD.
底面ABCD,底面ABCD∩平面PAD=AD,∴AB⊥平面PAD.
(2)取AD的中點F,連結AF,CF,∵平面PAD⊥平面ABCD,且PF⊥AD,
∴PF⊥平面BCD,∴CF是PC在平面ABCD上的射影,
∴∠PCF是直線PC與底面ABCD所成的角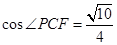
(3)設點D到平面PBC的距離為h,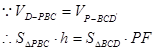
在△PBC中,易知PB=PC=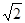 ,
,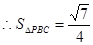
又

即點D到平面PBC的距離為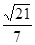
考點:本題考查了線面角的求法及點到面距離的問題
點評:對于距離問題往往通過轉化的方法簡化計算,這兩個問題是立體幾何中的重點問題,要求我們格外注意這類問題


科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
如圖所示,四棱錐P-ABCD的底面ABCD是邊長為1的菱形,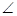 BCD=60
BCD=60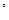 ,E是CD的中點,PA
,E是CD的中點,PA 底面ABCD,PA=2.
底面ABCD,PA=2.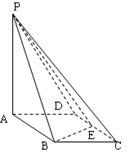
(1)證明:平面PBE 平面PAB;
平面PAB;
(2)求平面PAD和平面PBE所成二面角的正弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)在正四棱柱ABCD-A1B1C1D1中,E為CC1的中點.
(1)求證:AC1∥平面BDE;(2)求異面直線A1E與BD所成角。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題12分)如圖,在長方體ABCD-A1B1C1D1中,E, F分別是棱BC,CC1上的點,CF="AB=2CE," AB:AD:AA1=1:2:4.
(Ⅰ)求異面直線EF與A1D所成角的余弦值;
(Ⅱ)證明AF⊥平面A1ED;
(Ⅲ)求二面角A1-ED-F的正弦值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com