
()(本題14分)如圖,矩形ABCD和梯形BEFC所在平面互相垂直,
,∠BCF=∠CEF=90°,AD=![]()
(Ⅰ)求證:AE∥平面DCF;
(Ⅱ)當AB的長為何值時,二面角A-EF-C的大小為60°?
(Ⅰ)略(Ⅱ) 當AB為![]() 時,二面角A-EFC的大小為60°.
時,二面角A-EFC的大小為60°.
本題主要考查空間線面關系、空間向量的概念與運算等基礎知識,同時考查空間想象能力和推理運算能力。
方法一:
(Ⅰ)證明:過點E作EG⊥CF并CF于G,連結DG,可得四邊形BCGE為矩形。又ABCD為矩形,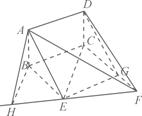 所以AD⊥∥EG,從而四邊形ADGE為平行四邊形,故AE∥DG。
所以AD⊥∥EG,從而四邊形ADGE為平行四邊形,故AE∥DG。
因為AE![]() 平面DCF,DG
平面DCF,DG![]() 平面DCF,所以AE∥平面DCF。
平面DCF,所以AE∥平面DCF。
(Ⅱ)解:過點B作BH⊥EF交FE的延長線于H,連結AH。
由平面ABCD⊥平面BEFG,AB⊥BC,得
AB⊥平面BEFC,
從而 AH⊥EF,
所以∠AHB為二面角A-EF-C的平面角。
在Rt△EFG中,因為EG=AD=![]()
又因為CE⊥EF,所以CF=4,
從而 BE=CG=3。
于是BH=BE·sin∠BEH=![]()
因為AB=BH·tan∠AHB,
所以當AB為![]() 時,二面角A-EF-G的大小為60°.
時,二面角A-EF-G的大小為60°.
 方法二:
方法二:
如圖,以點C為坐標原點,以CB、CF和CD分別
作為x軸、y軸和z軸,建立空間直角坐標系C-xyz.
設AB=a,BE=b,CF=c,
則C(0,0,0),A(![]()
![]()
(Ⅰ)證明:![]()
所以![]()
所以CB⊥平面ABE。
因為GB⊥平面DCF,所以平面ABE∥平面DCF
故AE∥平面DCF
(II)解:因為![]() ,
,
所以![]() ,從而
,從而
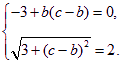
解得b=3,c=4.
所以![]() .
.
設![]() 與平面AEF垂直,
與平面AEF垂直,
則 ![]() ,
,
解得 ![]() .
.
又因為BA⊥平面BEFC,![]() ,
,
所以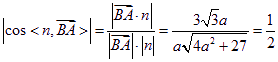 ,
,
得到 ![]() .
.
所以當AB為![]() 時,二面角A-EFC的大小為60°.
時,二面角A-EFC的大小為60°.


科目:高中數學 來源: 題型:
(本題14分)如圖,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中點.
 (1)FD∥平面ABC;
(1)FD∥平面ABC;
(2)AF⊥平面EDB.
查看答案和解析>>
科目:高中數學 來源:2011年廣東省揭陽市高二上學期期末檢測數學理卷 題型:解答題
(本題14分)如圖,在四棱錐 中,底面
中,底面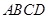 是邊長為1的菱形,
是邊長為1的菱形,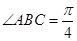 ,
, 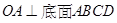 ,
, 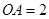 ,
,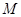 為
為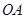 的中點,
的中點,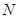 為
為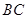 的中點.
的中點.
(Ⅰ)證明: ;
;
(Ⅱ)求異面直線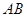 與
與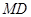 所成角的大小;
所成角的大小;
(Ⅲ)求點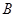 到平面
到平面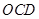 的距離.
的距離.
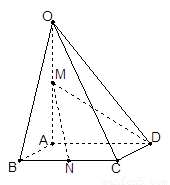
查看答案和解析>>
科目:高中數學 來源:2007年普通高等學校招生全國統一考試理科數學卷(浙江) 題型:解答題
(本題14分)如圖,直線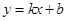 與橢圓
與橢圓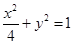 交于
交于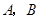 兩點,記
兩點,記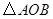 的面積為
的面積為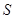 .
.
(I)求在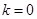 ,
,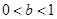 的條件下,
的條件下,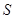 的最大值;
的最大值;
(II)當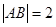 ,
,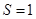 時,求直線
時,求直線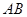 的方程.
的方程.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com