(本題14分)已知函數(shù)
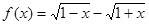
。
(Ⅰ)求函數(shù)
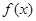
的定義域;
(Ⅱ)用定義判斷
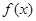
的奇偶性;
(Ⅰ)
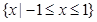
(Ⅱ)
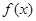
是奇函數(shù)
試題分析:(Ⅰ)由題意知要使函數(shù)有意義,
需要滿足
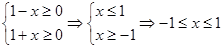
,
所以函數(shù)的定義域是
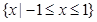
. ……6分
(Ⅱ)因為定義域為
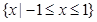
關于原點對稱, ……8分
又
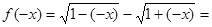
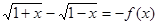
, ……12分
故
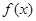
是奇函數(shù)。 ……14分
點評:求函數(shù)的定義域,只要讓每一部分都有意義即可,而且定義域必須寫成集合或區(qū)間的形式;要判斷函數(shù)的奇偶性,首先要判斷函數(shù)的定義域是否關于原點對稱.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題滿分13分)設函數(shù)
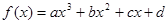
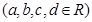
滿足:
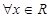
都有
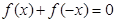
,且
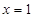
時,
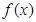
取極小值
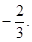
(1)
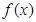
的解析式;
(2)當
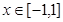
時,證明:函數(shù)圖象上任意兩點處的切線不可能互相垂直;
(3)設
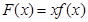
, 當
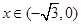
時,求函數(shù)
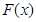
的最小值,并指出當
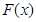
取最小值時相應的
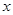
值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(1)(5分)若函數(shù)
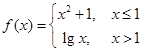
,則
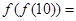
_______________.
(2)(5分)化簡:
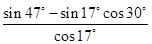
=____________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
比較大小:

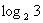
(填“>”或“<”).
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分14分)
已知函數(shù)f (x)=e
x,g(x)=lnx,h(x)=kx+b.
(1)當b=0時,若對
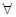
x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求實數(shù)k的取值范圍;
(2)設h(x)的圖象為函數(shù)f (x)和g(x)圖象的公共切線,切點分別為(x
1, f (x
1))和(x
2, g(x
2)),其中x
1>0.
①求證:x
1>1>x
2;
②若當x≥x
1時,關于x的不等式ax
2-x+xe
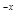
+1≤0恒成立,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知定義在
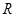
上的函數(shù)
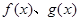
滿足
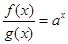
,且
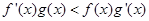
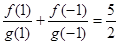
,若有窮數(shù)列
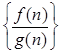
(
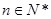
)的前
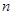
項和等于
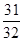
,則
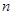
等于( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
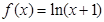
滿足0<
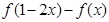
<1。
(1)求
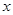
的取值范圍;
(2)若
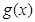
是偶函數(shù)且滿足
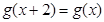
,當
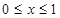
時,有
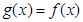
,求
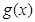
在
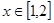
上的解析式。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知
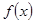
是定義在
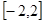
上的函數(shù),且對任意實數(shù)
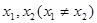
,恒有
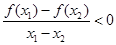
,且
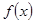
的最大值為1,則滿足
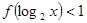
的解集為
.
查看答案和解析>>

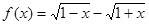 。
。 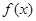 的定義域;
的定義域;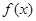 的奇偶性;
的奇偶性; 閱讀快車系列答案
閱讀快車系列答案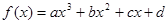
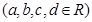 滿足:
滿足: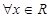 都有
都有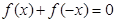 ,且
,且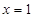 時,
時,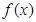 取極小值
取極小值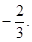
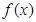 的解析式;
的解析式;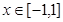 時,證明:函數(shù)圖象上任意兩點處的切線不可能互相垂直;
時,證明:函數(shù)圖象上任意兩點處的切線不可能互相垂直;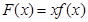 , 當
, 當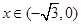 時,求函數(shù)
時,求函數(shù)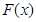 的最小值,并指出當
的最小值,并指出當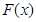 取最小值時相應的
取最小值時相應的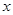 值.
值.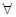 x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求實數(shù)k的取值范圍;
x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求實數(shù)k的取值范圍;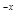 +1≤0恒成立,求實數(shù)a的取值范圍.
+1≤0恒成立,求實數(shù)a的取值范圍.