
已知函數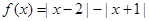 .
.
(1)求證: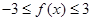 ;
;
(2)解不等式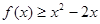
 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:高中數學 來源: 題型:解答題
已知二次函數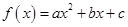 .
.
(1)若對任意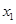 、
、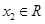 ,且
,且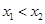 ,都有
,都有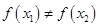 ,求證:關于
,求證:關于 的方程
的方程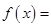
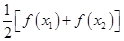 有兩個不相等的實數根且必有一個根屬于
有兩個不相等的實數根且必有一個根屬于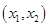 ;
;
(2)若關于 的方程
的方程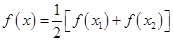 在
在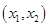 上的根為
上的根為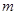 ,且
,且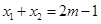 ,設函數
,設函數 的圖象的對稱軸方程為
的圖象的對稱軸方程為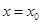 ,求證:
,求證: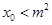 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 .
.
⑴ 求函數 的單調區間;
的單調區間;
⑵ 如果對于任意的 ,
, 總成立,求實數
總成立,求實數 的取值范圍;
的取值范圍;
⑶ 設函數 ,
, . 過點
. 過點 作函數
作函數 圖像的所有切線,令各切點的橫坐標構成數列
圖像的所有切線,令各切點的橫坐標構成數列 ,求數列
,求數列 的所有項之和
的所有項之和 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(14分)已知函數 ,其中a是實數.設A(x1,f(x1)),B(x2,f(x2))為該函數圖象上的兩點,且x1<x2.
,其中a是實數.設A(x1,f(x1)),B(x2,f(x2))為該函數圖象上的兩點,且x1<x2.
(Ⅰ)指出函數f(x)的單調區間;
(Ⅱ)若函數f(x)的圖象在點A,B處的切線互相垂直,且x2<0,證明:x2﹣x1≥1;
(Ⅲ)若函數f(x)的圖象在點A,B處的切線重合,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了降低能源損耗,某城市對新建住宅的屋頂和外墻都要求建造隔熱層.某幢建筑物要建造可使用20年的隔熱層,每厘米厚的隔熱層建造成本為6萬元.該建筑物每年的能源消耗費用C(單位:萬元)與隔熱層厚度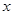 (單位:cm)滿足關系:
(單位:cm)滿足關系: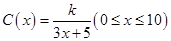 ,若不建隔熱層,每年能源消耗費用為8萬元.設
,若不建隔熱層,每年能源消耗費用為8萬元.設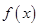 為隔熱層建造費用與20年的能源消耗費用之和.
為隔熱層建造費用與20年的能源消耗費用之和.
(1)求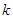 的值及
的值及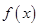 的表達式;
的表達式;
(2)隔熱層修建多厚時,總費用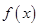 達到最小,并求最小值.
達到最小,并求最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設 是定義在
是定義在 的可導函數,且不恒為0,記
的可導函數,且不恒為0,記 .若對定義域內的每一個
.若對定義域內的每一個 ,總有
,總有 ,則稱
,則稱 為“
為“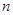 階負函數 ”;若對定義域內的每一個
階負函數 ”;若對定義域內的每一個 ,總有
,總有 ,則稱
,則稱 為“
為“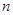 階不減函數”(
階不減函數”( 為函數
為函數 的導函數).
的導函數).
(1)若 既是“1階負函數”,又是“1階不減函數”,求實數
既是“1階負函數”,又是“1階不減函數”,求實數 的取值范圍;
的取值范圍;
(2)對任給的“2階不減函數” ,如果存在常數
,如果存在常數 ,使得
,使得 恒成立,試判斷
恒成立,試判斷 是否為“2階負函數”?并說明理由.
是否為“2階負函數”?并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com