
為了保護環(huán)境,某工廠在國家的號召下,把廢棄物回收轉(zhuǎn)化為某種產(chǎn)品,經(jīng)測算,處理成本 (萬元)與處理量
(萬元)與處理量 (噸)之間的函數(shù)關(guān)系可近似的表示為:
(噸)之間的函數(shù)關(guān)系可近似的表示為: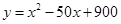 ,且每處理一噸廢棄物可得價值為
,且每處理一噸廢棄物可得價值為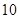 萬元的某種產(chǎn)品,同時獲得國家補貼
萬元的某種產(chǎn)品,同時獲得國家補貼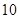 萬元.
萬元.
(1)當 時,判斷該項舉措能否獲利?如果能獲利,求出最大利潤;
時,判斷該項舉措能否獲利?如果能獲利,求出最大利潤;
如果不能獲利,請求出國家最少補貼多少萬元,該工廠才不會虧損?
(2)當處理量為多少噸時,每噸的平均處理成本最少?
(1)國家最少需要補貼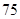 萬元,該工廠才能不會虧損;(2)30.
萬元,該工廠才能不會虧損;(2)30.
解析試題分析:(1)本題考查函數(shù)應用,屬于容易題,解題的關(guān)鍵是列出收益函數(shù),收益等于收入減成本,因此有利潤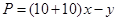 ,化簡后它是關(guān)于
,化簡后它是關(guān)于 的二次函數(shù),利用二次函數(shù)的知識求出
的二次函數(shù),利用二次函數(shù)的知識求出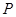 的取值范圍,如果
的取值范圍,如果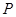 有非負的取值,就能說明可能獲利,如果
有非負的取值,就能說明可能獲利,如果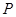 沒有非負取值,說明不能獲利,而國家最小補貼就是
沒有非負取值,說明不能獲利,而國家最小補貼就是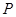 中最大值的絕對值.(2)每噸平均成本等于
中最大值的絕對值.(2)每噸平均成本等于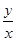 ,由題意
,由題意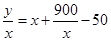 ,我們根據(jù)基本不等式的知識就可以求出它的最小值以及取最小值時的
,我們根據(jù)基本不等式的知識就可以求出它的最小值以及取最小值時的 值.
值.
試題解析:(1)根據(jù)題意得,利潤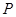 和處理量
和處理量 之間的關(guān)系:
之間的關(guān)系: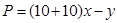
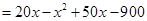
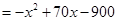 2分
2分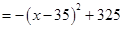 ,
,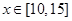 .
.
∵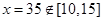 ,
,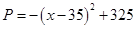 在
在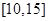 上為增函數(shù),
上為增函數(shù),
可求得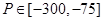 . 5分
. 5分
∴國家只需要補貼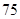 萬元,該工廠就不會虧損. 7分
萬元,該工廠就不會虧損. 7分
(2)設(shè)平均處理成本為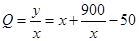 9分
9分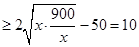 , 11分
, 11分
當且僅當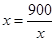 時等號成立,由
時等號成立,由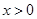 得
得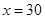 .
.
因此,當處理量為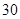 噸時,每噸的處理成本最少為
噸時,每噸的處理成本最少為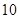 萬元. 14分
萬元. 14分
考點:函數(shù)應用題,二次函數(shù)的值域,基本不等式的應用.


科目:高中數(shù)學 來源: 題型:解答題
設(shè)二次函數(shù)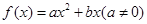 滿足條件:①
滿足條件:①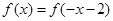 ;②函數(shù)
;②函數(shù) 的圖像與直線
的圖像與直線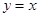 相切.
相切.
(1)求函數(shù) 的解析式;
的解析式;
(2)若不等式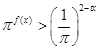 在
在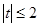 時恒成立,求實數(shù)
時恒成立,求實數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
定義在[﹣1,1]上的奇函數(shù)f(x)滿足f(1)=2,且當a,b∈[﹣1,1],a+b≠0時,有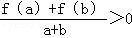 .
.
(1)試問函數(shù)f(x)的圖象上是否存在兩個不同的點A,B,使直線AB恰好與y軸垂直,若存在,求出A,B兩點的坐標;若不存在,請說明理由并加以證明.
(2)若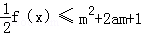 對所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求實數(shù)m的取值范圍.
對所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
某商品每件成本9元,售價為30元,每星期賣出144件. 如果降低價格,銷售量可以增加,且每星期多賣出的商品件數(shù)與商品單價的降低值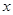 (單位:元,
(單位:元, )的平方成正比.
)的平方成正比.
已知商品單價降低2元時,一星期多賣出8件.
(1)將一個星期的商品銷售利潤表示成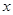 的函數(shù);
的函數(shù);
(2)如何定價才能使一個星期的商品銷售利潤最大?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù) .
.
(1)若 在
在 上存在零點,求實數(shù)
上存在零點,求實數(shù) 的取值范圍;
的取值范圍;
(2)當 時,若對任意的
時,若對任意的 ,總存在
,總存在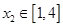 使
使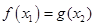 成立,求實數(shù)
成立,求實數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
某公司為一家制冷設(shè)備廠設(shè)計生產(chǎn)某種型號的長方形薄板,其周長為4m.這種薄板須沿其對角線折疊后使用.如圖所示,ABCD(AB>AD)為長方形薄板,沿AC折疊后AB′交DC于點P.當△ADP的面積最大時最節(jié)能,凹多邊形ACB′PD的面積最大時制冷效果最好.
(1)設(shè)AB=xm,用x表示圖中DP的長度,并寫出x的取值范圍;
(2)若要求最節(jié)能,應怎樣設(shè)計薄板的長和寬?
(3)若要求制冷效果最好,應怎樣設(shè)計薄板的長和寬?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)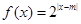 和函數(shù)
和函數(shù)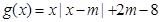 ,其中
,其中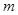 為參數(shù),且滿足
為參數(shù),且滿足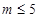 .
.
(1)若 ,寫出函數(shù)
,寫出函數(shù)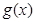 的單調(diào)區(qū)間(無需證明);
的單調(diào)區(qū)間(無需證明);
(2)若方程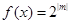 在
在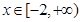 上有唯一解,求實數(shù)
上有唯一解,求實數(shù)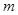 的取值范圍;
的取值范圍;
(3)若對任意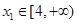 ,存在
,存在 ,使得
,使得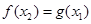 成立,求實數(shù)
成立,求實數(shù)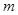 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com