
定義在 上的函數
上的函數 同時滿足以下條件:
同時滿足以下條件:
① 在(0,1)上是減函數,在(1,+∞)上是增函數;
在(0,1)上是減函數,在(1,+∞)上是增函數;
② 是偶函數;
是偶函數;
③ 在x=0處的切線與直線
在x=0處的切線與直線 y=x+2垂直.
y=x+2垂直.
(1)求函數 =
= 的解析式;
的解析式;
(2)設g(x)= ,若存在實數x∈[1,e],使
,若存在實數x∈[1,e],使 <
< ,求實數m的取值范圍.
,求實數m的取值范圍.
(1) ;(2)
;(2)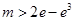 .
.
解析試題分析:(1)利用已知條件可知f′(x)=3ax2+2bx+c中b=0,且f′(1)=3a+2b+c=0,另外根據條件③知f′(0)=c=-1,從而能夠求出a,b,c的值;(2)對于恒成立求參數m的取值范圍,可以利用分離參數法,得到m>xlnx-x3+x,構造函數M(x)=xlnx-x3+x,通過兩次求導,得到M(x)在[1,e]上遞減,且M(x)的最小值為2e-e3,故m>2e-e3.
試題解析:(1)f′(x)=3ax2+2bx+c,∵f(x)在(0,1)上是減函數,在(1,+∞)上是增函數,
∴f′(1)=3a+2b+c=0①
由f′(x)是偶函數得:b=0②
又f(x)在x=0處的切線與直線y=x+2垂直,f′(0)=c=-1③
由①②③得:a=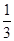 ,b=0,c=-1,即f(x)=
,b=0,c=-1,即f(x)=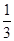 x3-x+3.
x3-x+3.
(2)由已知得:存在實數x∈[1,e],使lnx-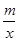 <x2-1
<x2-1
即存在x∈[1,e],使m>xlnx-x3+x
設M(x)=xlnx-x3+x x∈[1,e],則M′(x)=lnx-3x2+2
設H(x)=lnx-3x2+2,則H′(x)=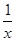 -6x=
-6x=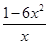
∵x∈[1,e],∴H′(x)<0,即H(x)在[1,e]上遞減
于是,H(x)≤H(1),即H(x)≤-1<0,即M′(x)<0
∴M(x)在[1,e]上遞減,∴M(x)≥M(e)=2e-e3
于是有m>2e-e3為所求.
考點:1.函數的奇偶性與利用導函數求最值;2.恒成立求參數取值范圍問題.


 優質課堂快樂成長系列答案
優質課堂快樂成長系列答案科目:高中數學 來源: 題型:解答題
某地政府為科技興市,欲在如圖所示的矩形ABCD的非農業用地中規劃出一個高科技工業園區(如圖中陰影部分),形狀為直角梯形QPRE(線段EQ和RP為兩個底邊),已知 其中AF是以A為頂點、AD為對稱軸的拋物線段.試求該高科技工業園區的最大面積.
其中AF是以A為頂點、AD為對稱軸的拋物線段.試求該高科技工業園區的最大面積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數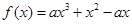 ,其中
,其中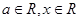 .
.
(1)當 時,求函數
時,求函數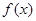 在
在 處的切線方程;
處的切線方程;
(2)若函數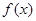 在區間(1,2)上不是單調函數,試求
在區間(1,2)上不是單調函數,試求 的取值范圍;
的取值范圍;
(3)已知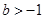 ,如果存在
,如果存在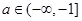 ,使得函數
,使得函數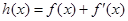
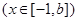 在
在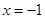 處取得最小值,試求
處取得最小值,試求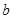 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
學校操場邊有一條小溝,溝沿是兩條長150米的平行線段,溝寬 為2米,,與溝沿垂直的平面與溝的交線是一段拋物線,拋物線的頂點為
為2米,,與溝沿垂直的平面與溝的交線是一段拋物線,拋物線的頂點為 ,對稱軸與地面垂直,溝深2米,溝中水深1米.
,對稱軸與地面垂直,溝深2米,溝中水深1米.
(Ⅰ)求水面寬;
(Ⅱ)如圖1所示形狀的幾何體稱為柱體,已知柱體的體積為底面積乘以高,求溝中的水有多少立方米?
(Ⅲ)現在學校要把這條水溝改挖(不準填土)成截面為等腰梯形的溝,使溝的底面與地面平行,溝深不變,兩腰分別與拋物線相切(如圖2),問改挖后的溝底寬為多少米時,所挖的土最少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數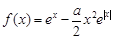 .
.
(Ⅰ)若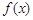 是
是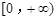 上是增函數,求實數a的取值范圍;
上是增函數,求實數a的取值范圍;
(Ⅱ)證明:當a≥1時,證明不等式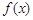 ≤x+1對x∈R恒成立;
≤x+1對x∈R恒成立;
(Ⅲ)對于在(0,1)中的任一個常數a,試探究是否存在x0>0,使得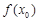 >x0+1成立?如果存在,請求出符合條件的一個x0;如果不存在,請說明理由.
>x0+1成立?如果存在,請求出符合條件的一個x0;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 ,
, .
.
(1)若 ,則
,則 ,
, 滿足什么條件時,曲線
滿足什么條件時,曲線 與
與 在
在 處總有相同的切線?
處總有相同的切線?
(2)當 時,求函數
時,求函數 的單調減區間;
的單調減區間;
(3)當 時,若
時,若 對任意的
對任意的 恒成立,求
恒成立,求 的取值的集合.
的取值的集合.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 ,
, ,
, ,其中
,其中 ,且
,且 .
.
⑴當 時,求函數
時,求函數 的最大值;
的最大值;
⑵求函數 的單調區間;
的單調區間;
⑶設函數 若對任意給定的非零實數
若對任意給定的非零實數 ,存在非零實數
,存在非零實數 (
( ),使得
),使得 成立,求實數
成立,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數f(x)=ax-(1+a2)x2,其中a>0,區間I={x|f(x)>0}.
(1)求I的長度(注:區間(α,β)的長度定義為β-α);
(2)給定常數k∈(0,1),當1-k≤a≤1+k時,求I長度的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com