
已知數列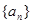 滿足
滿足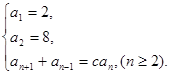 (
(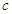 為常數,
為常數,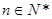 )
)
(1)當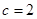 時,求
時,求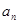 ;
;
(2)當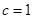 時,求
時,求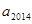 的值;
的值;
(3)問:使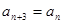 恒成立的常數
恒成立的常數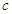 是否存在?并證明你的結論.
是否存在?并證明你的結論.
(1)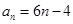 ;(2)
;(2) ;(3)存在
;(3)存在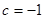
解析試題分析:(1)由 ,所以
,所以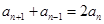 ,
,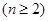 .所以數列
.所以數列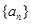 是一個等差數列.首項為2,公差為6,所以可求得通項公式.
是一個等差數列.首項為2,公差為6,所以可求得通項公式.
(2)由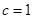 ,由于需要求
,由于需要求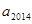 的值,所以考慮數列
的值,所以考慮數列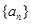 的周期性,通過列舉即可得到數列
的周期性,通過列舉即可得到數列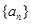 的周期為6.從而可求得
的周期為6.從而可求得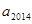 的值.
的值.
(3)假設存在常數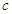 使得
使得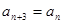 恒成立.由
恒成立.由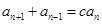 ,向前遞推一個式子,再利用
,向前遞推一個式子,再利用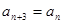 將得到兩個關于
將得到兩個關于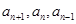 的等式,從而消去一個即可得到
的等式,從而消去一個即可得到 ,或
,或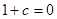 .由于
.由于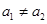 .所以只有
.所以只有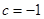 .再結合已知即可得到結論.
.再結合已知即可得到結論.
試題解析:(1)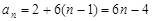
(2)  ,
, ,
,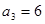 ,
, ,
,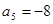 ,
,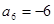 ,
, ,
, ,
, ,
,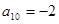 ,
,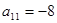 ,
,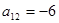 ,我們發現數列為一周期為6的數列.事實上,由
,我們發現數列為一周期為6的數列.事實上,由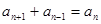 有
有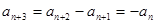 ,
, .……8分(理由和結論各2分)
.……8分(理由和結論各2分)
因為 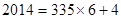 ,所以
,所以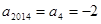 .
.
(3)假設存在常數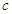 ,使
,使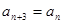 恒成立.
恒成立.
由 ①,
①,
及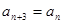 ,有
,有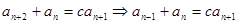 ②
②
1式減2式得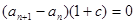 .
.
所以 ,或
,或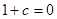 .
.
當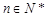 ,
, 時,數列{
時,數列{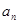 }為常數數列,不滿足要求.
}為常數數列,不滿足要求.
由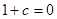 得
得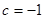 ,于是
,于是 ,即對于
,即對于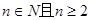 ,都有
,都有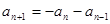 ,所以
,所以 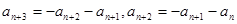 ,從而
,從而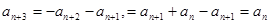
 .
.
所以存在常數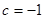 ,使
,使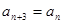 恒成立.
恒成立.
考點:1.等差數列的判斷.2.數列的周期性.3.數列恒成立問題.4.遞推的思想.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com