
已知四棱錐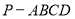 ,
,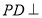 面
面 ,
,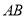 ∥
∥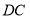 ,
, ,
,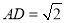 ,
,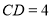 ,
,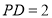 ,
,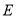 為
為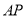 上一點,
上一點,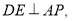
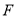 是平面
是平面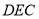 與
與 的交點.
的交點.

(1)求證: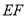 ∥
∥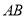 ;
;
(2)求證: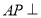 面
面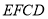 ;
;
(3)求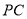 與面
與面 所成角的正弦值.
所成角的正弦值.
(1)、(2)證明詳見解析;(3)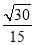 .
.
【解析】
試題分析:(1)首先根據 ∥
∥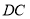 ,可證明
,可證明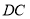 ∥面
∥面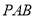 ,再利用線面平行的關系可證明
,再利用線面平行的關系可證明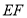 ∥
∥ ;(2)考慮通過證明
;(2)考慮通過證明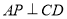 與
與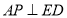 (已知),而證明
(已知),而證明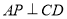 可通過證明
可通過證明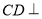 面
面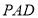 來證明;(3)考慮以DA,DC,DP為坐標建立空間直角坐標,通過求直線PC的方向向量與平面EFCD的法向量的夾角來處理.
來證明;(3)考慮以DA,DC,DP為坐標建立空間直角坐標,通過求直線PC的方向向量與平面EFCD的法向量的夾角來處理.
試題解析:(1) ∥
∥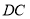 ,
,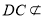 面
面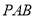 ,
,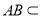 面
面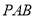 ,∴
,∴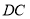 ∥面
∥面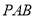 ,
,
又∵面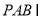 面
面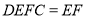 ,
,
∴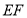 ∥
∥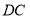 ,∴
,∴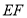 ∥
∥ .
.
(2)∵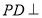 面
面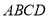 ,∴
,∴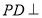
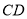 .
.
又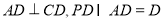 ,∴
,∴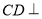 面
面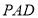 ,
,
∵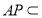 面
面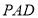 ,∴
,∴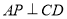 .
.
又∵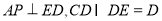 ,∴
,∴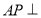 面
面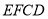 .
.
(3)以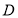 為原點,
為原點,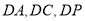 分別為
分別為 軸建立空間直角坐標系,
軸建立空間直角坐標系,
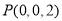
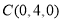
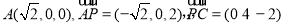 ,
,
設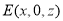 由
由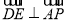 且
且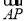 ∥
∥ 可得
可得
 ,解得
,解得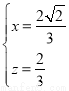 ,∴
,∴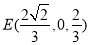 .
.
設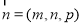 為平面
為平面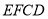 的一個法向量則有
的一個法向量則有
 ,令
,令 ,
,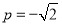 ,∴
,∴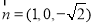 ,
,
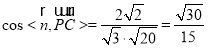
∴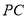 與面
與面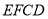 所成角的正弦值為
所成角的正弦值為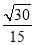 .
.
考點:1、空間直線、平面間的平行與垂直;2、直線與平面所成角;3、空間向量的應用.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源:2015屆山東省文登市高二上學期期末統考文科數學試卷(解析版) 題型:選擇題
不等式 表示的平面區域是以直線
表示的平面區域是以直線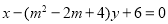 為界的兩個平面區域中的一個,且點
為界的兩個平面區域中的一個,且點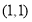 在這個區域內,則實數
在這個區域內,則實數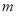 的取值范圍是( )
的取值范圍是( )
A.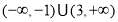 B.
B. 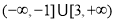 C.
C.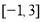 D.
D. 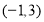
查看答案和解析>>
科目:高中數學 來源:2015屆山東威海高二上學期期末考試理科數學試卷(解析版) 題型:填空題
設 滿足約束條件
滿足約束條件 ,若目標函數
,若目標函數 的最大值為
的最大值為 ,則
,則 的最小值為________________.
的最小值為________________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com