
已知動圓M過定點P(0,m)(m>0),且與定直線![]() 相切,動圓圓心M的軌跡方程為C,直線
相切,動圓圓心M的軌跡方程為C,直線![]() 過點P 交曲線C于A、B兩點。
過點P 交曲線C于A、B兩點。
(1)若![]() 交
交![]() 軸于點S,求
軸于點S,求![]() 的取值范圍;
的取值范圍;
(2)若![]() 的傾斜角為
的傾斜角為![]() ,在
,在![]() 上是否存在點E使△ABE為正三角形? 若能,求點E的坐標;若不能,說明理由.
上是否存在點E使△ABE為正三角形? 若能,求點E的坐標;若不能,說明理由.
(1) ![]() (2)直線l上不存在點E,使得△ABE是正三角形
(2)直線l上不存在點E,使得△ABE是正三角形
(1)依題意,曲線C是以點P為焦點,直線![]() 為準線的拋物線,
為準線的拋物線,
所以曲線C的方程為![]() ……(2分)
……(2分)
設![]() 方程為
方程為![]() 代入
代入![]() 由消去
由消去![]() 得
得![]()
設![]() 、
、![]() ,則
,則![]() ……(3分)
……(3分)
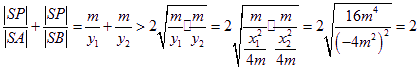
所以![]() 的取值范圍是
的取值范圍是![]() ……(7分)
……(7分)
(2)由(1)知![]() 方程為
方程為![]() 代入
代入![]() 由消去
由消去![]() 得
得![]()
![]() ,
,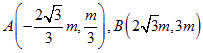 ……(8分)
……(8分)
假設存在點![]() ,使△ABE為正三角形,則|BE|=|AB|且|AE|=|AB,……(9分)
,使△ABE為正三角形,則|BE|=|AB|且|AE|=|AB,……(9分)
![]() 即
即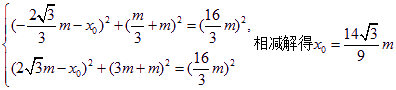 ……(11分)
……(11分)
若 ,則
,則![]()
因此,直線l上不存在點E,使得△ABE是正三角形. ……(12分)
解法二:設AB的中點為G,則 ……(8分)
……(8分)
由![]() 聯立
聯立![]() 方程
方程
![]() 與
與![]() 方程求得
方程求得 ……(10分)
……(10分)
由![]() 得
得![]() ,矛盾
,矛盾
因此,直線l上不存在點E,使得△ABE是正三角形. ……(12分)


科目:高中數學 來源: 題型:
| |SP| |
| |SA| |
| |SP| |
| |SB| |
查看答案和解析>>
科目:高中數學 來源: 題型:
| |SP| |
| |SA| |
| |SP| |
| |SB| |
查看答案和解析>>
科目:高中數學 來源:2010年山東省青島市高三質量檢測數學試卷3(理科)(解析版) 題型:解答題
 ,求l2的方程.(3)若l2的傾斜角為30°,在l1上是否存在點E使△ABE為正三角形?若能,求點E的坐標;若不能,說明理由.
,求l2的方程.(3)若l2的傾斜角為30°,在l1上是否存在點E使△ABE為正三角形?若能,求點E的坐標;若不能,說明理由.查看答案和解析>>
科目:高中數學 來源:2010年安徽省宿州市蕭縣中學高考數學三模試卷(解析版) 題型:解答題
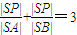 ,求l2的方程.
,求l2的方程.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com