中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

設(shè)函數(shù)f(x)=sin2ωx+2sinωx·cosωx-cos2ωx+λ(x∈R)的圖象關(guān)于直線x=π對(duì)稱,其中ω,λ為常數(shù),且ω∈(,1).
(1)求函數(shù)f(x)的最小正周期;
(2)若y=f(x)的圖象經(jīng)過點(diǎn)(,0),求函數(shù)f(x)的值域.

(1) 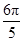   (2) [-2-,2-]

解析解:(1)f(x)=sin2ωx-cos2ωsinx+2sinωx·cosωx+λ
=-cos2ωx+sin2ωx+λ
=2sin(2ωx-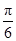)+λ.
由直線x=π是y=f(x)圖象的一條對(duì)稱軸,
可得sin(2ωπ-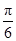)=±1,
所以2ωπ-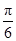=kπ+(k∈Z),
即ω=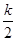+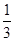(k∈Z).
又ω∈(,1),k∈Z,
所以k=1,故ω=.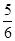
所以f(x)的最小正周期是.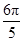
(2)由y=f(x)的圖象過點(diǎn)(,0),
得f()=0,
即λ=-2sin(×-)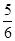
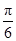=-2sin=-,
即λ=-.
故f(x)=2sin(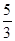x-)-.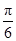
所以函數(shù)f(x)的值域?yàn)閇-2-,2-].

練習(xí)冊(cè)系列答案
相關(guān)習(xí)題

科目：高中數(shù)學(xué) 來源： 題型：解答題

已知向量,設(shè)函數(shù).
(1).求函數(shù)f(x)的最小正周期;
(2).已知a,b,c分別為三角形ABC的內(nèi)角對(duì)應(yīng)的三邊長(zhǎng),A為銳角,a=1,，且恰是函數(shù)f(x)在上的最大值,求A,b和三角形ABC的面積.

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

已知向量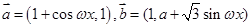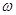（為常數(shù)且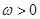），函數(shù)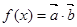在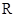上的最大值為．
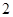（1）求實(shí)數(shù)的值；
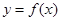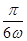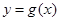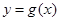（2）把函數(shù)的圖象向右平移個(gè)單位，可得函數(shù)的圖象，若在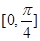上為增函數(shù)，求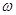取最大值時(shí)的單調(diào)增區(qū)間．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

設(shè)向量，，
（1）若，求的值；
（2）設(shè)函數(shù)，求的最大值。

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

已知，，，為坐標(biāo)原點(diǎn).
（1），求的值；
（2）若，且，求與的夾角.

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

已知函數(shù)f(x)=cosx·cos(x-).
(1)求f的值;
(2)求使f(x)<成立的x的取值集合.

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

已知函數(shù)f(x)＝2sin x(sin x＋cos x)．
(1)求函數(shù)f(x)的最小正周期和最大值；
(2)在給出的平面直角坐標(biāo)系中，畫出函數(shù)y＝f(x)在區(qū)間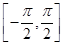上的圖象．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

已知ω＞0，a＝(2sinωx＋cosωx，2sinωx－cosωx)，b＝(sinωx，cosωx)．f(x)＝a·b.f(x)圖象上相鄰的兩個(gè)對(duì)稱軸的距離是.
(1)求ω的值；
(2)求函數(shù)f(x)在區(qū)間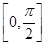上的最大值和最小值．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

已知α是三角形的內(nèi)角，且sinα＋cosα＝.
(1)求tanα的值；
(2)將用tanα表示出來，并求其值．

查看答案和解析>>

同步練習(xí)冊(cè)答案