
(本題滿分10分)選修4 -4 :坐標(biāo)系與參數(shù)方程
將圓 上各點的縱坐標(biāo)壓縮至原來的
上各點的縱坐標(biāo)壓縮至原來的 ,所得曲線記作C;將直線3x-2y-8=0
,所得曲線記作C;將直線3x-2y-8=0
繞原點逆時針旋轉(zhuǎn)90°所得直線記作l
.(I)求直線l與曲線C的方程;
(II)求C上的點到直線l的最大距離.
.(I) 曲線C: ;直線l :
;直線l :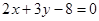 ;(II)
;(II) 。
。
解析試題分析:(Ⅰ)設(shè)曲線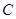 上任一點為
上任一點為 ,則
,則 在圓
在圓 上,
上,
于是 即
即 .
.
直線 的極坐標(biāo)方程為
的極坐標(biāo)方程為 ,將其記作
,將其記作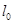 ,
,
設(shè)直線上任一點為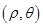 ,則點
,則點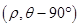 在
在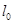 上,
上,
于是 ,即:
,即: ,
,
故直線的方程為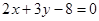 ; …5分
; …5分
(Ⅱ)設(shè)曲線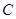 上任一點為
上任一點為 ,
,
它到直線的距離為 ,
,
其中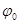 滿足:
滿足: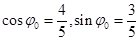 .
.
∴當(dāng) 時,
時, . …10分
. …10分
考點:直線的極坐標(biāo)方程;直線與橢圓的位置關(guān)系;橢圓的標(biāo)準(zhǔn)方程。
點評:本題主要考查了直線與橢圓的極坐標(biāo)方程的靈活應(yīng)用。考查了學(xué)生分析問題的能力及數(shù)學(xué)化歸思想.


 奪冠訓(xùn)練單元期末沖刺100分系列答案
奪冠訓(xùn)練單元期末沖刺100分系列答案 新思維小冠軍100分作業(yè)本系列答案
新思維小冠軍100分作業(yè)本系列答案 名師指導(dǎo)一卷通系列答案
名師指導(dǎo)一卷通系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
已知曲線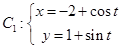 (
(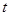 為參數(shù)),
為參數(shù)),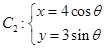 (
(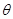 為參數(shù)).
為參數(shù)).
(1)化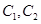 的方程為普通方程,并說明它們分別表示什么曲線;
的方程為普通方程,并說明它們分別表示什么曲線;
(2)過曲線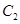 的左頂點且傾斜角為
的左頂點且傾斜角為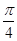 的直線
的直線 交曲線
交曲線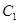 于
于 兩點,求
兩點,求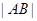 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知曲線 的極坐標(biāo)方程為
的極坐標(biāo)方程為 ,以極點為原點,極軸為軸的正半軸建立直角坐標(biāo)系,直線
,以極點為原點,極軸為軸的正半軸建立直角坐標(biāo)系,直線 的參數(shù)方程
的參數(shù)方程
(Ⅰ)寫出直線 的普通方程與曲線
的普通方程與曲線 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(Ⅱ)設(shè)曲線 經(jīng)過伸縮變換
經(jīng)過伸縮變換 得到曲線
得到曲線 ,在曲線
,在曲線 上求一點
上求一點 ,使點
,使點 到直線
到直線 的距離最小,并求出最小距離.
的距離最小,并求出最小距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
[選修4 - 4:坐標(biāo)系與參數(shù)方程](本小題滿分10分)
在直角坐標(biāo)系 中,直線
中,直線 的參數(shù)方程為
的參數(shù)方程為 (
( 為參數(shù)),若以直角坐標(biāo)系
為參數(shù)),若以直角坐標(biāo)系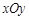 的
的 點為極點,
點為極點,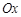 為極軸,且長度單位相同,建立極坐標(biāo)系,得曲線
為極軸,且長度單位相同,建立極坐標(biāo)系,得曲線 的極坐標(biāo)方程為
的極坐標(biāo)方程為 .直線
.直線 與曲線
與曲線 交于
交于 兩點,求
兩點,求 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分10分)
在極坐標(biāo)系中,點 坐標(biāo)是
坐標(biāo)是 ,曲線
,曲線 的方程為
的方程為 ;以極點為坐標(biāo)原點,極軸為
;以極點為坐標(biāo)原點,極軸為 軸的正半軸建立平面直角坐標(biāo)系,斜率是
軸的正半軸建立平面直角坐標(biāo)系,斜率是 的直線
的直線 經(jīng)過點
經(jīng)過點 .
.
(1)寫出直線 的參數(shù)方程和曲線
的參數(shù)方程和曲線 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)求證直線 和曲線
和曲線 相交于兩點
相交于兩點 、
、 ,并求
,并求 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分10分)選修4-4:坐標(biāo)系與參數(shù)方程
已知極坐標(biāo)系的極點與直角坐標(biāo)系的原點重合,極軸與直角坐標(biāo)系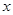 軸的正半軸重合.直線的參數(shù)方程是
軸的正半軸重合.直線的參數(shù)方程是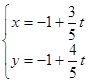 (
(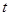 為參數(shù)),曲線
為參數(shù)),曲線 的極坐標(biāo)方程為
的極坐標(biāo)方程為 .
.
(Ⅰ)求曲線 的直角坐標(biāo)方程;(Ⅱ)設(shè)直線與曲線
的直角坐標(biāo)方程;(Ⅱ)設(shè)直線與曲線 相交于
相交于 兩點,求
兩點,求 兩點間的距離.
兩點間的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
在回歸分析中,代表了數(shù)據(jù)點和它在回歸直線上相應(yīng)位置的差異的是( )
| A.總偏差平方和 | B.殘差平方和 | C.回歸平方和 | D.相關(guān)指數(shù)R2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
在第29屆北京奧運會上,中國健兒取得了51金、21銀、28銅的好成績,穩(wěn)居金牌榜榜首,由此許多人認(rèn)為中國進(jìn)入了世界體育強(qiáng)國之列,也有許多人持反對意見,有網(wǎng)友為此進(jìn)行了調(diào)查,在參加調(diào)查的2548名男性中有1560名持反對意見,2452名女性中有1200名持反對意見,在運用這些數(shù)據(jù)說明性別對判斷“中國進(jìn)入了世界體育強(qiáng)國之列”是否有關(guān)系時,用什么方法最有說服力( )
| A.平均數(shù)與方差 | B.回歸直線方程 | C.獨立性檢驗 | D.概率 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com