
已知函數(shù)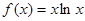 .
.
(1)求 的單調區(qū)間和極值;
的單調區(qū)間和極值;
(2)設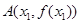 ,
,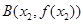 ,且
,且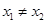 ,證明:
,證明: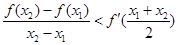 .
.
(1)單調增區(qū)間是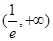 ,單調減區(qū)間是
,單調減區(qū)間是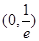 ;極小值
;極小值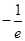 ,無極大值。(2)詳見解析
,無極大值。(2)詳見解析
解析試題分析:(1)先求導,再令導數(shù)大于0的函數(shù)的增區(qū)間,令導數(shù)小于0得函數(shù)的減區(qū)間,根據(jù)函數(shù)的單調性可得函數(shù)的極值。(2)即證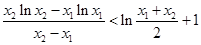 ,不妨設
,不妨設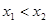 ,問題可轉化為
,問題可轉化為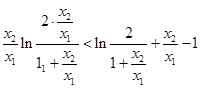 ,令
,令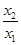
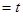 ,令
,令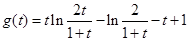 ,用導數(shù)求其最值,證其最大值小于0即可。
,用導數(shù)求其最值,證其最大值小于0即可。
試題解析:(1)定義域為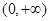
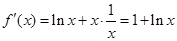
令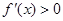 則
則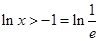 ∴
∴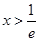 ;令
;令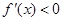 則
則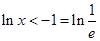 ∴
∴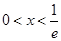
∴ 的單調增區(qū)間是
的單調增區(qū)間是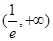 ,單調減區(qū)間是
,單調減區(qū)間是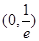
 極小值
極小值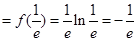 ,
, 無極大值
無極大值
(2)證明:不妨設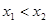 ,
,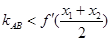
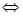
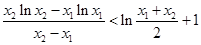
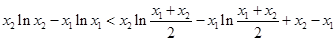
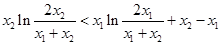
兩邊同除以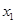 得,
得,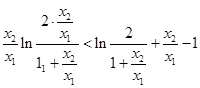
令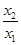
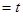 ,則
,則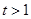 ,即證:
,即證: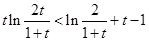
令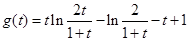
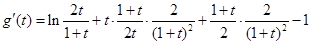
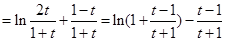
令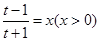 ,
,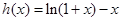
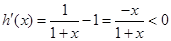 ,
, 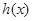 在
在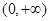 上單調遞減,所以
上單調遞減,所以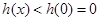
即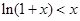 ,即
,即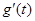
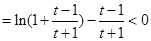 恒成立
恒成立
∴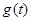 在
在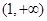 上是減函數(shù),所以
上是減函數(shù),所以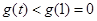
∴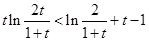 得證
得證
所以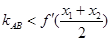 成立
成立
考點:利用導數(shù)研究函數(shù)的單調性和極值最值問題。


 名校提分一卷通系列答案
名校提分一卷通系列答案 課程達標測試卷闖關100分系列答案
課程達標測試卷闖關100分系列答案 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關100分系列答案
全能闖關100分系列答案科目:高中數(shù)學 來源: 題型:解答題
經銷商用一輛 型卡車將某種水果運送(滿載)到相距400km的水果批發(fā)市場.據(jù)測算,
型卡車將某種水果運送(滿載)到相距400km的水果批發(fā)市場.據(jù)測算, 型卡車滿載行駛時,每100km所消耗的燃油量
型卡車滿載行駛時,每100km所消耗的燃油量 (單位:
(單位: )與速度
)與速度 (單位:km/h)的關系近似地滿足
(單位:km/h)的關系近似地滿足 ,除燃油費外,人工工資、車損等其他費用平均每小時300元.已知燃油價格為7.5元/L.
,除燃油費外,人工工資、車損等其他費用平均每小時300元.已知燃油價格為7.5元/L.
(1)設運送這車水果的費用為 (元)(不計返程費用),將
(元)(不計返程費用),將 表示成速度
表示成速度 的函數(shù)關系式;
的函數(shù)關系式;
(2)卡車該以怎樣的速度行駛,才能使運送這車水果的費用最少?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)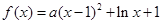 .
.
(1)當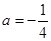 時,求函數(shù)
時,求函數(shù)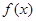 的極值;
的極值;
(2)若函數(shù)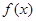 在區(qū)間
在區(qū)間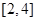 上是減函數(shù),求實數(shù)
上是減函數(shù),求實數(shù) 的取值范圍;
的取值范圍;
(3)當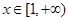 時,函數(shù)
時,函數(shù)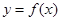 圖像上的點都在
圖像上的點都在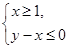 所表示的平面區(qū)域內,求實數(shù)
所表示的平面區(qū)域內,求實數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
設f(x)=ax3+bx+c(a≠0)為奇函數(shù),其圖象在點(1,f(1))處的切線與直線x-6y-7=0垂直,導函數(shù)f′(x)的最小值為-12.
(1)求函數(shù)f(x)的解析式;
(2)求函數(shù)f(x)的單調增區(qū)間,并求函數(shù)f(x)在[-1,3]上的最大值和最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)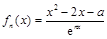 ,其中
,其中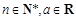 ,
,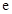 是自然對數(shù)的底數(shù).
是自然對數(shù)的底數(shù).
(1)求函數(shù)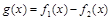 的零點;
的零點;
(2)若對任意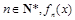 均有兩個極值點,一個在區(qū)間(1,4)內,另一個在區(qū)間[1,4]外,求a的取值范圍;
均有兩個極值點,一個在區(qū)間(1,4)內,另一個在區(qū)間[1,4]外,求a的取值范圍;
(3)已知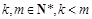 ,且函數(shù)
,且函數(shù)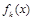 在R上是單調函數(shù),探究函數(shù)
在R上是單調函數(shù),探究函數(shù)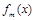 的單調性.
的單調性.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)
(1)求曲線y=f(x)在(2,f(2))處的切線方程;
(2)若g(x)=f(x)一 有兩個不同的極值點.其極小值為M,試比較2M與一3的大小,并說明理由;
有兩個不同的極值點.其極小值為M,試比較2M與一3的大小,并說明理由;
(3)設q>p>2,求證:當x∈(p,q)時, .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
設函數(shù)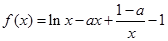 .
.
(Ⅰ)當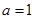 時,求曲線
時,求曲線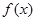 在
在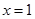 處的切線方程;
處的切線方程;
(Ⅱ)當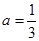 時,求函數(shù)
時,求函數(shù)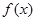 的單調區(qū)間;
的單調區(qū)間;
(Ⅲ)在(Ⅱ)的條件下,設函數(shù)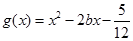 ,若對于
,若對于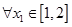 ,
,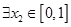 ,使
,使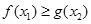 成立,求實數(shù)
成立,求實數(shù)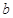 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com