已知
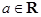
,函數(shù)
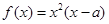
,若
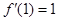
.
(1)求
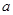
的值并求曲線
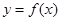
在點
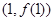
處的切線方程
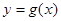
;
(2)設
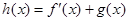
,求
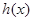
在
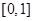
上的最大值與最小值.
試題分析:解:(1)
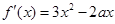
,由
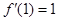
得

,所以
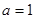
;
當
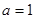
時,
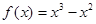
,
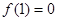
,又
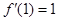
,
所以曲線
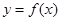
在

處的切線方程為
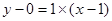
,即
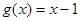
; 6分
(2)由(1)得
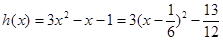
,
又
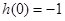
,
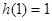
,
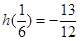
,
∴
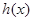
在
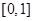
上有最大值1,有最小值

.- 12分
點評:主要是根據(jù)導數(shù)的幾何意義求解切線方程以及函數(shù)的最值,屬于中檔題。
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:填空題
已知函數(shù)f(x)=x3+ax2+x+2(a>0)的極大值點和極小值點都在區(qū)間(-1,1)內,則實數(shù)a的取值范圍是______.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設函數(shù)

有三個零點

,且

則下列結論正確的是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若
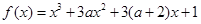
有極大值和極小值,則
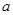
的取值范圍是 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知
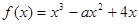
有兩個極值點
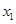
、
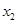
,且
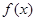
在區(qū)間(0,1)上有極大值,無極小值,則實數(shù)
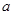
的取值范圍是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
函數(shù)

在

內有極小值,則實數(shù)
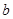
的取值范圍
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題滿分12分) 設函數(shù)
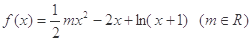
.
(Ⅰ)判斷
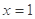
能否為函數(shù)
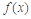
的極值點,并說明理由;
(Ⅱ)若存在
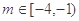
,使得定義在
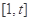
上的函數(shù)
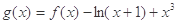
在
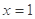
處取得最大值,求實數(shù)
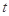
的最大值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
函數(shù)
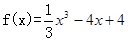
在
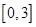
上的最大值是( )
A.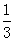 | B. 4 | C.-4 | D.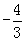 |
查看答案和解析>>

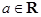 ,函數(shù)
,函數(shù)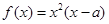 ,若
,若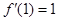 .
.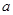 的值并求曲線
的值并求曲線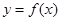 在點
在點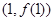 處的切線方程
處的切線方程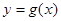 ;
;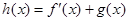 ,求
,求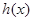 在
在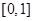 上的最大值與最小值.
上的最大值與最小值.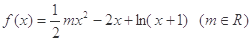 .
.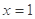 能否為函數(shù)
能否為函數(shù)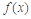 的極值點,并說明理由;
的極值點,并說明理由;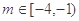 ,使得定義在
,使得定義在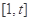 上的函數(shù)
上的函數(shù)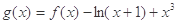 在
在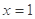 處取得最大值,求實數(shù)
處取得最大值,求實數(shù)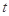 的最大值.
的最大值.