
若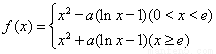 ,其中
,其中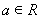 .
.
(1)當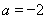 時,求函數
時,求函數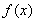 在區間
在區間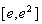 上的最大值;
上的最大值;
(2)當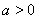 時,若
時,若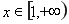 ,
,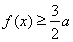 恒成立,求
恒成立,求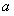 的取值范圍.
的取值范圍.
 名師點撥卷系列答案
名師點撥卷系列答案 英才計劃期末調研系列答案
英才計劃期末調研系列答案科目:高中數學 來源:2014年高考數學全程總復習課時提升作業七十二第十章第九節練習卷(解析版) 題型:解答題
某商店儲存的50個燈泡中,甲廠生產的燈泡占60%,乙廠生產的燈泡占40%,甲廠生產的燈泡的一等品率是90%,乙廠生產的燈泡的一等品率是80%.
(1)若從這50個燈泡中隨機抽取出1個燈泡(每個燈泡被取出的機會均等),則它是甲廠生產的一等品的概率是多少?
(2)若從這50個燈泡中隨機抽取出2個燈泡(每個燈泡被取出的機會均等),這2個燈泡中是甲廠生產的一等品的個數記為ξ,求E(ξ)的值.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業七十七選修4-4第一節練習卷(解析版) 題型:解答題
已知☉O1和☉O2的極坐標方程分別是ρ=2cosθ和ρ=2asinθ(a是非零常數).
(1)將兩圓的極坐標方程化為直角坐標方程.
(2)若兩圓的圓心距為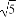 ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中數學 來源:2014年高中數學全國各省市理科導數精選22道大題練習卷(解析版) 題型:解答題
設函數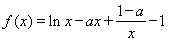 .
.
(Ⅰ)當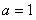 時,求曲線
時,求曲線 在
在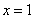 處的切線方程;
處的切線方程;
(Ⅱ)當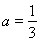 時,求函數
時,求函數 的單調區間;
的單調區間;
(Ⅲ)在(Ⅱ)的條件下,設函數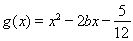 ,若對于
,若對于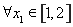 ,
,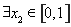 ,使
,使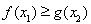 成立,求實數
成立,求實數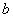 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2014年高中數學全國各省市理科導數精選22道大題練習卷(解析版) 題型:解答題
設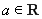 ,函數
,函數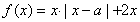 .
.
(1)若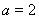 ,求函數
,求函數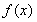 在區間
在區間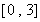 上的最大值;
上的最大值;
(2)若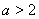 ,寫出函數
,寫出函數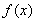 的單調區間(不必證明);
的單調區間(不必證明);
(3)若存在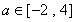 ,使得關于
,使得關于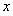 的方程
的方程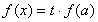 有三個不相等的實數解,求實數
有三個不相等的實數解,求實數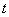 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2014年高中數學全國各省市理科導數精選22道大題練習卷(解析版) 題型:解答題
已知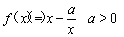 ,
,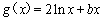 ,且直線
,且直線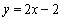 與曲線
與曲線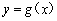 相切.
相切.
(1)若對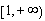 內的一切實數
內的一切實數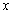 ,不等式
,不等式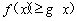 恒成立,求實數
恒成立,求實數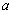 的取值范圍;
的取值范圍;
(2)當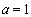 時,求最大的正整數
時,求最大的正整數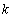 ,使得對
,使得對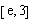 (
(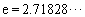 是自然對數的底數)內的任意
是自然對數的底數)內的任意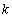 個實數
個實數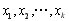 都有
都有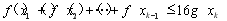 成立;
成立;
(3)求證: .
.
查看答案和解析>>
科目:高中數學 來源:2014年陜西省咸陽市高考模擬考試(一)理科數學試卷(解析版) 題型:填空題
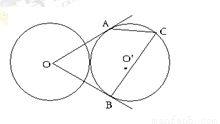
如圖,兩個等圓⊙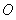 與⊙
與⊙ 外切,過
外切,過 作⊙
作⊙ 的兩條切線
的兩條切線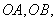
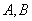 是切點,點
是切點,點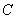 在圓
在圓 上且不與點
上且不與點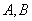 重合,則
重合,則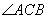 = .
= .
查看答案和解析>>
科目:高中數學 來源:2014年廣東省廣州市畢業班綜合測試一理科數學試卷(解析版) 題型:解答題
已知函數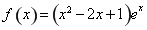 (其中
(其中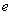 為自然對數的底數).
為自然對數的底數).
(1)求函數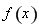 的單調區間;
的單調區間;
(2)定義:若函數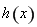 在區間
在區間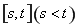 上的取值范圍為
上的取值范圍為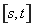 ,則稱區間
,則稱區間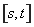 為函數
為函數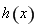 的“域同區間”.試問函數
的“域同區間”.試問函數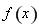 在
在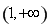 上是否存在“域同區間”?若存在,求出所有符合條件的“域同區間”;若不存在,請說明理由.
上是否存在“域同區間”?若存在,求出所有符合條件的“域同區間”;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com