
已知函數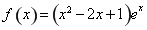 (其中
(其中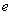 為自然對數的底數).
為自然對數的底數).
(1)求函數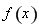 的單調區間;
的單調區間;
(2)定義:若函數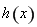 在區間
在區間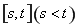 上的取值范圍為
上的取值范圍為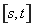 ,則稱區間
,則稱區間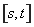 為函數
為函數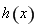 的“域同區間”.試問函數
的“域同區間”.試問函數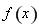 在
在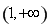 上是否存在“域同區間”?若存在,求出所有符合條件的“域同區間”;若不存在,請說明理由.
上是否存在“域同區間”?若存在,求出所有符合條件的“域同區間”;若不存在,請說明理由.
(1)單調遞增區間為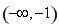 和
和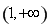 ,單調遞減區間為
,單調遞減區間為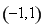 ;(2)詳見解析.
;(2)詳見解析.
【解析】
試題分析:(1)先求出函數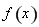 的定義域與導數,求出極值點,解有關導數的不等式,從而確定函數
的定義域與導數,求出極值點,解有關導數的不等式,從而確定函數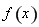 的單調增區間和減區間;(2)結合(1)中的結論可知,函數
的單調增區間和減區間;(2)結合(1)中的結論可知,函數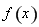 在區間
在區間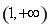 上單調遞增,根據定義得到
上單調遞增,根據定義得到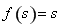 ,
,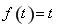 ,問題轉化為求方程
,問題轉化為求方程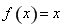 在區間
在區間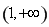 上的實數根,結合導數來討論方程
上的實數根,結合導數來討論方程 在區間
在區間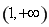 上的實根的個數,從而確定函數
上的實根的個數,從而確定函數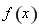 在區間
在區間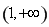 上是否存在“域同區間”.
上是否存在“域同區間”.
試題解析:(1)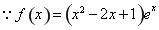 ,定義域為
,定義域為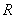 ,
,
且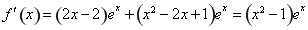 ,
,
令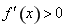 ,即
,即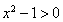 ,解得
,解得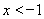 或
或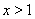 ;令
;令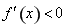 ,即
,即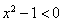 ,解得
,解得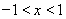 ,
,
故函數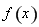 的單調遞增區間為
的單調遞增區間為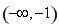 和
和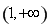 ,單調遞減區間為
,單調遞減區間為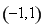 ;
;
(2)由(1)知,函數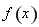 在區間
在區間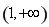 上是單調遞增函數,
上是單調遞增函數,
假設函數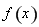 在區間
在區間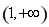 上存在“域同區間”
上存在“域同區間”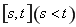 ,則有
,則有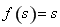 ,
,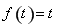 ,
,
則方程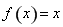 在區間
在區間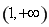 上有兩個相異實根,
上有兩個相異實根,
構造新函數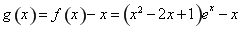 ,定義域為
,定義域為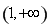 ,
,
則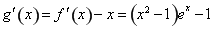 ,
,
設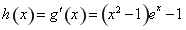 ,則
,則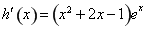 ,
,
當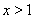 時,
時,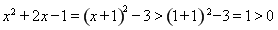 ,則
,則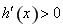 恒成立,
恒成立,
因此函數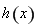 在區間
在區間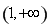 上單調遞增,
上單調遞增, ,
,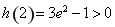 ,
,
故函數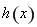 在區間
在區間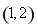 上存在唯一零點
上存在唯一零點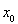 ,則有
,則有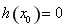 ,
,
當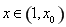 時,
時,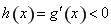 ;當
;當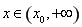 時,
時,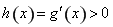 ,
,
故函數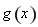 在區間
在區間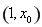 上是單調遞減函數,在區間
上是單調遞減函數,在區間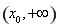 上是單調遞增函數,
上是單調遞增函數,
因為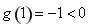 ,
,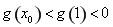 ,
,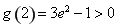 ,
,
所以函數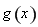 在區間
在區間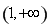 有且只有一個零點,
有且只有一個零點,
這與方程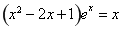 有兩個大于
有兩個大于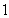 的實根相矛盾,所以假設不成立!
的實根相矛盾,所以假設不成立!
所以函數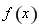 在區間
在區間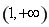 上不存在“域同區間”.
上不存在“域同區間”.
考點:1.利用導數求函數的單調區間;2.新定義;3.函數的零點


 新編小學單元自測題系列答案
新編小學單元自測題系列答案 字詞句段篇系列答案
字詞句段篇系列答案科目:高中數學 來源:2014年高考數學全程總復習課時提升作業七十三第十章第十節練習卷(解析版) 題型:選擇題
在調查學生數學成績與物理成績之間的關系時,得到如下數據(人數):
| 物理 成績好 | 物理 成績不好 | 合計 |
數學成績好 | 62 | 23 | 85 |
數學成績不好 | 28 | 22 | 50 |
合計 | 90 | 45 | 135 |
那么有把握認為數學成績與物理成績之間有關的百分比為( )
(A)25% (B)75% (C)95% (D)99%
查看答案和解析>>
科目:高中數學 來源:2014年高中數學全國各省市理科導數精選22道大題練習卷(解析版) 題型:解答題
若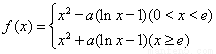 ,其中
,其中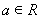 .
.
(1)當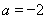 時,求函數
時,求函數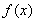 在區間
在區間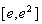 上的最大值;
上的最大值;
(2)當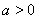 時,若
時,若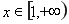 ,
,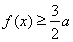 恒成立,求
恒成立,求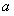 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2014年陜西省咸陽市高考模擬考試(一)理科數學試卷(解析版) 題型:填空題
設命題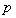 :實數
:實數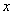 滿足
滿足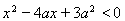 ,其中
,其中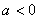 ;命題
;命題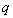 :實數
:實數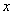 滿足
滿足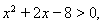 且
且 的必要不充分條件,則實數
的必要不充分條件,則實數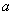 的取值范圍是 .
的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源:2014年陜西省咸陽市高考模擬考試(一)理科數學試卷(解析版) 題型:選擇題
某幾何體的三視圖如右圖(其中側視圖中的圓弧是半圓),則該幾何體的表面積為( )
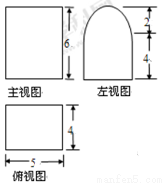
A.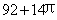 B.
B.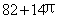 C.
C.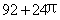 D.
D.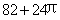
查看答案和解析>>
科目:高中數學 來源:2014年廣東省廣州市畢業班綜合測試一理科數學試卷(解析版) 題型:解答題
已知函數 的圖象經過點
的圖象經過點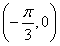 .
.
(1)求實數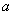 的值;
的值;
(2)設 ,求函數
,求函數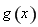 的最小正周期與單調遞增區間.
的最小正周期與單調遞增區間.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年(安徽專用)高考數學(文)仿真模擬卷1練習卷(解析版) 題型:填空題
“求方程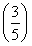 x+
x+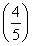 x=1的解”有如下解題思路:設f(x)=
x=1的解”有如下解題思路:設f(x)=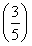 x+
x+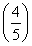 x,則f(x)在R上單調遞減,且f(2)=1,所以原方程有唯一解x=2.類比上述解題思路,不等式x6-(x+2)>(x+2)3-x2的解集是________.
x,則f(x)在R上單調遞減,且f(2)=1,所以原方程有唯一解x=2.類比上述解題思路,不等式x6-(x+2)>(x+2)3-x2的解集是________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com