
在平面直角坐標系xOy中,點P是圓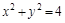 上一動點,
上一動點,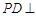 x軸于點D.記滿足
x軸于點D.記滿足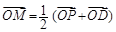 的動點M的軌跡為Γ.
的動點M的軌跡為Γ.
(1)求軌跡Γ的方程;
(2)已知直線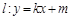 與軌跡Γ交于不同兩點A,B,點G是線段AB中點,射線OG交軌跡Γ于點Q,且
與軌跡Γ交于不同兩點A,B,點G是線段AB中點,射線OG交軌跡Γ于點Q,且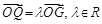 .
.
①證明: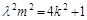
②求△AOB的面積S(λ)的解析式,并計算S(λ)的最大值.
(1)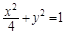 ;(2)
;(2)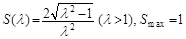
解析試題分析:(1)由已知M是PD的中點,利用P點在圓上,可以求出M的點軌跡方程為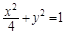 ;(2)點Q在(1)中的橢圓上,G是OQ上的分點,利用直線與橢圓的關系,可以找到λ與m和k的關系,并進一步將三角形AOB的面積表示成λ的函數關系式,再求出它的最大值.
;(2)點Q在(1)中的橢圓上,G是OQ上的分點,利用直線與橢圓的關系,可以找到λ與m和k的關系,并進一步將三角形AOB的面積表示成λ的函數關系式,再求出它的最大值.
試題解析:(1)設 ,則點
,則點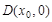 ,且
,且 (1)
(1)
∵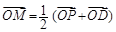
∴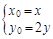 (2)
(2)
將(2)代入(1),得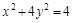
∴軌跡Γ的方程為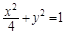 ; 5分
; 5分
(2)①令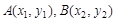
由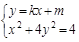 消去y
消去y
得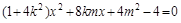 6分
6分
∴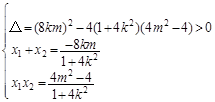 ,即
,即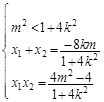 (3)
(3)
∴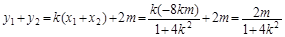
又由中點坐標公式,得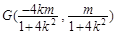
根據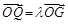 ,得
,得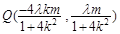
將其代入橢圓方程,有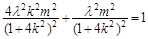
化簡得: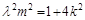 (4) 9分
(4) 9分
②由(3)(4)得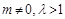
∵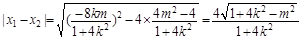 (5)
(5)
在△AOB中,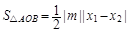 (6)
(6)
∴由(4)(5)(6)可得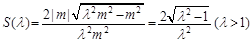 12分
12分
令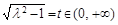
則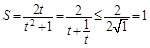 (當且僅當t=1時,即
(當且僅當t=1時,即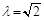 時取“=”)
時取“=”)
∴當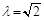 時,
時,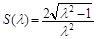 取得最大值,其最大值為1. 13分
取得最大值,其最大值為1. 13分
考點:動點軌跡,直線與橢圓的位置關系,中點坐標,平面向量的坐標運算,基本不等式,范圍與最值.


 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com