
已知函數 .
.
(1)若 的定義域和值域均是
的定義域和值域均是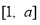 ,求實數
,求實數 的值;
的值;
(2)若 在區間
在區間 上是減函數,且對任意的
上是減函數,且對任意的 ,都有
,都有 ,求實數
,求實數 的取值范圍;
的取值范圍;
(3)若 ,且對任意的
,且對任意的 ,都存在
,都存在 ,使得
,使得 成立,求實數
成立,求實數 的取值范圍.
的取值范圍.
(1)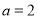 ;(2)
;(2)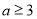 ;(3)
;(3)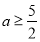 .
.
【解析】
試題分析:(1)先利用二次函數的性質確定函數 的單調遞減區間為
的單調遞減區間為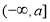 ,故
,故 在
在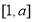 單調遞減,然后由定義域與值域列出等式關系,從而求解即可;(2)由(1)可知
單調遞減,然后由定義域與值域列出等式關系,從而求解即可;(2)由(1)可知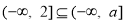 ,初步確定
,初步確定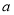 的取值范圍
的取值范圍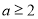 ,然后確定
,然后確定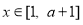 時函數
時函數 的最大值
的最大值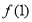 ,從中求解不等式組
,從中求解不等式組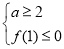 即可;(3)將“對任意的
即可;(3)將“對任意的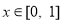 ,都存在
,都存在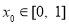 ,使得
,使得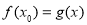 成立”轉化為
成立”轉化為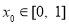 時,
時,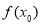 的值域包含了
的值域包含了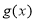 在
在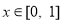 的值域,然后進行分別求
的值域,然后進行分別求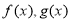 在
在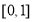 的值域,從集合間的包含關系即可求出
的值域,從集合間的包含關系即可求出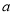 的取值范圍.
的取值范圍.
試題解析:(1)∵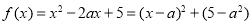
∴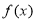 在
在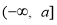 上單調遞減,又
上單調遞減,又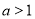 ,∴
,∴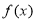 在
在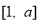 上單調遞減,
上單調遞減,
∴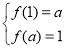 ,∴
,∴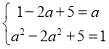 ,∴
,∴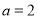 4分
4分
(2)∵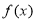 在區間
在區間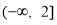 上是減函數,∴
上是減函數,∴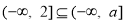 ,∴
,∴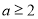
∴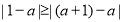 ,
,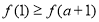
∴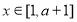 時,
時,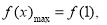
又∵對任意的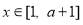 ,都有
,都有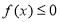 ,
,
∴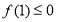 ,即
,即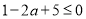 ,也就是
,也就是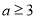
綜上可知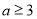 8分
8分
(3)∵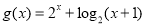 在
在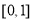 上遞增,
上遞增,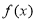 在
在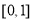 上遞減,
上遞減,
當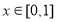 時,
時,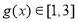 ,
,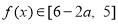
∵對任意的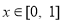 ,都存在
,都存在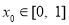 ,使得
,使得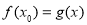 成立
成立
∴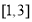
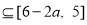
∴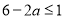 ,所以
,所以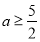 13分
13分
考點:1.二次函數圖像與性質;2.函數的單調性;3.函數與方程的問題.


 新思維假期作業寒假吉林大學出版社系列答案
新思維假期作業寒假吉林大學出版社系列答案科目:高中數學 來源:2016屆湖南省高一上學期期末考試數學試卷(解析版) 題型:選擇題
把正方形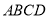 沿對角線
沿對角線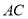 折起,當以
折起,當以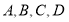 四點為頂點的三棱錐體積最大時,直線
四點為頂點的三棱錐體積最大時,直線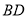 和平面
和平面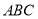 所成的角的大小為( )
所成的角的大小為( )
A.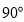 B.
B.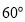 C.
C.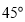 D.
D.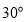
查看答案和解析>>
科目:高中數學 來源:2016屆湖北荊州中學高一上學期期中考試理科數學試卷(解析版) 題型:選擇題
下列說法正確的個數是( )
①空集是任何集合的真子集;
②函數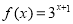 是指數函數;
是指數函數;
③既是奇函數又是偶函數的函數有無數多個;
④若 ,則
,則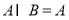
A.0個 B.1個 C.2個 D.3個
查看答案和解析>>
科目:高中數學 來源:2016屆湖北武漢部分重點中學高一上期末理數學卷(解析版) 題型:選擇題
給出以下命題:
①若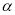 、
、 均為第一象限角,且
均為第一象限角,且 ,且
,且 ;
;
②若函數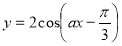 的最小正周期是
的最小正周期是 ,則
,則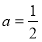 ;
;
③函數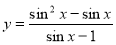 是奇函數;
是奇函數;
④函數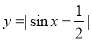 的周期是
的周期是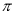 ;
;
⑤函數 的值域是
的值域是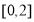 .
.
其中正確命題的個數為( )
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com