
已知函數
(1)若函數 在點
在點 處的切線與圓
處的切線與圓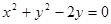 相切,求
相切,求 的值;
的值;
(2)當 時,函數
時,函數 的圖像恒在坐標軸
的圖像恒在坐標軸 軸的上方,試求出
軸的上方,試求出 的取值范圍.
的取值范圍.
(1)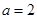 ;(2)
;(2)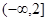 .
.
解析試題分析:本題綜合考查函數與導數及運用導數研究函數的單調區間、最值等數學知識和方法,突出考查綜合運用數學知識和方法分析問題、解決問題的能力,考查函數思想、分類討論思想.第一問,先將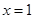 代入
代入 中,得到切點的縱坐標,對
中,得到切點的縱坐標,對 求導,將
求導,將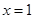 代入得到切線的斜率,所以點斜式寫出切線方程,因為它與圓相切,所以圓心到切線的距離等于半徑,列出表達式,求出
代入得到切線的斜率,所以點斜式寫出切線方程,因為它與圓相切,所以圓心到切線的距離等于半徑,列出表達式,求出 ;第二問,對
;第二問,對 求導,通過分析可轉化為當
求導,通過分析可轉化為當 時,
時,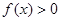 恒成立,設
恒成立,設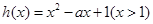 ,討論
,討論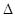 ,討論
,討論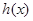 的正負,通過拋物線的性質,求最小值.
的正負,通過拋物線的性質,求最小值.
試題解析:(1) 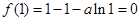 ,而
,而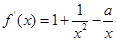 ,故
,故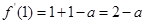 ,
,
所以 在點
在點 處的切線方程為
處的切線方程為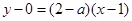 ,即
,即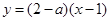 ,
,
由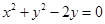 ,配方得
,配方得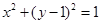 ,故該圓的圓心為
,故該圓的圓心為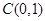 ,半徑
,半徑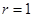 ,
,
由題意可知,圓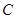 與直線
與直線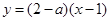 相切,所以
相切,所以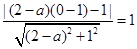 ,
,
即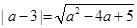 ,解得
,解得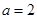 .
.
(2)函數 的定義域為
的定義域為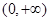 ,
,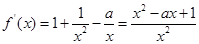 ,
,
由題意,只需當 時,
時,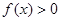 恒成立.
恒成立.
設 (
(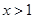 ),
), ,
,
當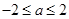 時,
時,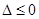 ,當
,當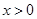 時,
時, 恒成立,即
恒成立,即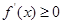 恒成立,
恒成立,
故 在
在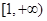 上是增函數,∴當
上是增函數,∴當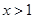 時,
時,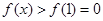 ,
,
當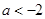 時,函數
時,函數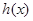 的對稱軸
的對稱軸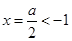 ,則
,則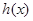 在
在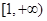 上是增函數,
上是增函數,
當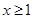 時,
時,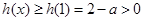 ,∴
,∴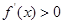 ,∴
,∴ 在
在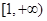 上是增函數,
上是增函數,
∴當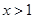 時,
時,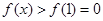 ,
,
當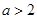 時,函數
時,函數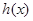 的對稱軸
的對稱軸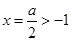 ,
,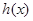 在
在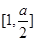 是減函數,
是減函數, ,
,
故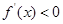 ,∴
,∴ 在
在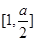 是減函數,
是減函數,
∴當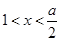 時,
時,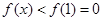 與當
與當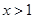 時,
時,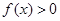 矛盾,
矛盾,
綜上所述, 的取值范圍是
的取值范圍是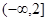 .
.
考點:1.利用導數求切線的方程;2.點到直線的距離公式;3.利用導數求函數最值.


 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案 單元加期末復習先鋒大考卷系列答案
單元加期末復習先鋒大考卷系列答案科目:高中數學 來源: 題型:解答題
某出版社新出版一本高考復習用書,該書的成本為5元/本,經銷過程中每本書需付給代理商m元(1≤m≤3)的勞務費,經出版社研究決定,新書投放市場后定價為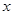 元/本(9≤
元/本(9≤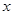 ≤11),預計一年的銷售量為
≤11),預計一年的銷售量為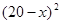 萬本.
萬本.
(1)求該出版社一年的利潤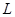 (萬元)與每本書的定價
(萬元)與每本書的定價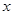 的函數關系式;
的函數關系式;
(2)當每本書的定價為多少元時,該出版社一年的利潤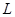 最大,并求出
最大,并求出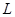 的最大值
的最大值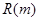 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某廠生產產品x件的總成本 (萬元),已知產品單價P(萬元)與產品件數x滿足:
(萬元),已知產品單價P(萬元)與產品件數x滿足: ,生產100件這樣的產品單價為50萬元,產量定為多少件時總利潤最大?
,生產100件這樣的產品單價為50萬元,產量定為多少件時總利潤最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com