
已知二次函數 ,及函數
,及函數 。
。
關于 的不等式
的不等式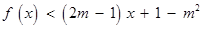 的解集為
的解集為 ,其中
,其中 為正常數。
為正常數。
(1)求 的值;
的值;
(2) R
R 如何取值時,函數
如何取值時,函數

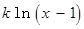 存在極值點,并求出極值點;
存在極值點,并求出極值點;
(3)若 ,且
,且
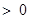 ,求證:
,求證:
 。
。
科目:高中數學 來源: 題型:解答題
某單位決定投資3200元建一倉庫(長方體狀),高度恒定,它的后墻利用舊墻,地面利用原地面均不花錢,正面用鐵柵,每米長造價40元,兩側墻砌磚,每米長造價45元,屋頂每平方米造價20元.
(1)倉庫面積 的最大允許值是多少?
的最大允許值是多少?
(2)為使面積 達到最大而實際投入又不超過預算,正面鐵柵應設計為多長?
達到最大而實際投入又不超過預算,正面鐵柵應設計為多長?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
將邊長為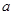 米的一塊正方形鐵皮的四角各截去一個大小相同的小正方形,然后將四邊折起做成一個無蓋的方盒.欲使所得的方盒有最大容積,截去的小正方形的邊長應為多少米?方盒的最大容積為多少?
米的一塊正方形鐵皮的四角各截去一個大小相同的小正方形,然后將四邊折起做成一個無蓋的方盒.欲使所得的方盒有最大容積,截去的小正方形的邊長應為多少米?方盒的最大容積為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數 ,
, 是定義域為R上的奇函數.
是定義域為R上的奇函數.
(1)求 的值,并證明當
的值,并證明當 時,函數
時,函數 是R上的增函數;
是R上的增函數;
(2)已知 ,函數
,函數 ,
, ,求
,求 的值域;
的值域;
(3)若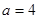 ,試問是否存在正整數
,試問是否存在正整數 ,使得
,使得 對
對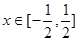 恒成立?若存在,請求出所有的正整數
恒成立?若存在,請求出所有的正整數 ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了保護環境,發展低碳經濟,某單位在國家科研部門的支持下,進行技術攻關,采用了新工藝,把二氧化碳轉化為一種可利用的化工產品.已知該單位每月的處理量最少為400噸,最多為600噸,月處理成本 (元)與月處理量
(元)與月處理量 (噸)之間的函數關系可近似的表示為:
(噸)之間的函數關系可近似的表示為: ,且每處理一噸二氧化碳得到可利用的化工產品價值為100元.
,且每處理一噸二氧化碳得到可利用的化工產品價值為100元.
(1)該單位每月處理量為多少噸時,才能使每噸的平均處理成本最低?
(2)該單位每月能否獲利?如果獲利,求出最大利潤;如果不獲利,則國家至少需要補貼多少元才能使該單位不虧損?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
經市場調查:生產某產品需投入年固定成本為3萬元,每生產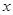 萬件,需另投入流動成本為
萬件,需另投入流動成本為 萬元,在年產量不足8萬件時,
萬元,在年產量不足8萬件時,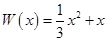 (萬元),在年產量不小于8萬件時,
(萬元),在年產量不小于8萬件時,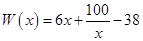 (萬元). 通過市場分析,每件產品售價為5元時,生產的商品能當年全部售完.
(萬元). 通過市場分析,每件產品售價為5元時,生產的商品能當年全部售完.
(1)寫出年利潤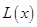 (萬元)關于年產量
(萬元)關于年產量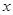 (萬件)的函數解析式;
(萬件)的函數解析式;
(注:年利潤=年銷售收入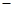 固定成本
固定成本 流動成本)
流動成本)
(2)年產量為多少萬件時,在這一商品的生產中所獲利潤最大?最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com