
已知函數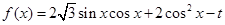 .
.
(Ⅰ)若方程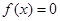 在
在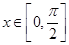 上有解,求
上有解,求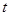 的取值范圍;
的取值范圍;
(Ⅱ)在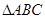 中,
中,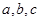 分別是A,B,C所對的邊,若
分別是A,B,C所對的邊,若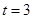 ,且
,且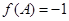 ,
,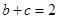 ,求
,求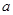 的最小值.
的最小值.
 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:高中數學 來源: 題型:解答題
設函數f(θ)=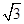 sinθ+cosθ,其中,角θ的頂點與坐標原點重合,始邊與x軸非負半軸重合,終邊經過點P(x,y),且0≤θ≤π.
sinθ+cosθ,其中,角θ的頂點與坐標原點重合,始邊與x軸非負半軸重合,終邊經過點P(x,y),且0≤θ≤π.
(1)若點P的坐標為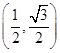 ,求f(θ)的值;
,求f(θ)的值;
(2)若點P(x,y)為平面區域Ω: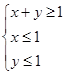 ,上的一個動點,試確定角θ的取值范圍,并求函數f(θ)的最小值和最大值.
,上的一個動點,試確定角θ的取值范圍,并求函數f(θ)的最小值和最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知向量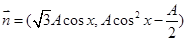 ,
,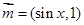 ,
,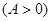 ,函數
,函數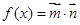 的最大值為
的最大值為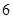 .
.
(Ⅰ)求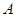 ;
;
(Ⅱ)將函數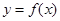 的圖像向左平移
的圖像向左平移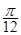 個單位,再將所得圖像上各點的橫坐標縮短為原來的
個單位,再將所得圖像上各點的橫坐標縮短為原來的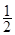 倍,縱坐標不變,得到函數
倍,縱坐標不變,得到函數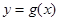 的圖像,求
的圖像,求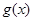 在
在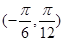 上的值域.
上的值域.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com