
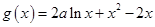 .
.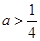 時,討論函數
時,討論函數 的單調性;
的單調性;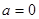 時,在函數
時,在函數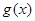 圖象上取不同兩點A、B,設線段AB的中點為
圖象上取不同兩點A、B,設線段AB的中點為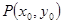 ,試探究函數
,試探究函數 在Q
在Q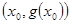 點處的切線與直線AB的位置關系?
點處的切線與直線AB的位置關系?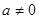 時
時 圖象是否存在不同的兩點A、B具有(2)問中所得出的結論.
圖象是否存在不同的兩點A、B具有(2)問中所得出的結論. 在定義域
在定義域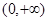 上單調遞增;(2)函數在Q點處的切線與直線AB平行;
上單調遞增;(2)函數在Q點處的切線與直線AB平行; 圖象不存在不同的兩點A、B具有(2)問中所得出的結論.
圖象不存在不同的兩點A、B具有(2)問中所得出的結論.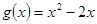 在點Q
在點Q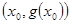 處的切線的斜率,再求出直線AB的斜率,可看出它們是相等的,所以函數在Q點處的切線與直線AB平行;
處的切線的斜率,再求出直線AB的斜率,可看出它們是相等的,所以函數在Q點處的切線與直線AB平行;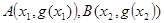
 ,若
,若 滿足(2)中結論,則有
滿足(2)中結論,則有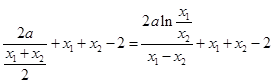 ,化簡得
,化簡得 (*).如果這個等式能夠成立,則存在,如果這個等式不能成立,則不存在.設
(*).如果這個等式能夠成立,則存在,如果這個等式不能成立,則不存在.設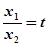 ,則*式整理得
,則*式整理得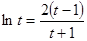 ,問題轉化成該方程在
,問題轉化成該方程在 上是否有解.再設函數
上是否有解.再設函數 ,下面通過導數即可知方程
,下面通過導數即可知方程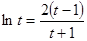 在
在 上是否有解,從而可確定函數
上是否有解,從而可確定函數 是否滿足(2)中結論.
是否滿足(2)中結論.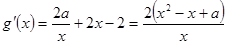 ,
,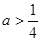 時,
時,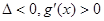 ,函數
,函數 在定義域
在定義域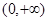 上單調遞增; 4分
上單調遞增; 4分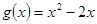 ,
, ,
,
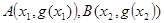
 ,若
,若 滿足(2)中結論,有
滿足(2)中結論,有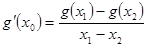 ,即
,即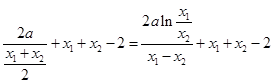
 (*) .9分
(*) .9分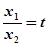 ,則*式整理得
,則*式整理得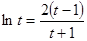 ,問題轉化成該方程在
,問題轉化成該方程在 上是否有解; 11分
上是否有解; 11分 ,則
,則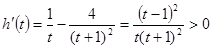 ,所以函數
,所以函數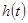 在
在 單調遞增,即
單調遞增,即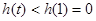 ,即方程
,即方程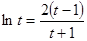 在
在 上無解,即函數
上無解,即函數 不滿足(2)中結論. 14分
不滿足(2)中結論. 14分

科目:高中數學 來源:不詳 題型:解答題
 ,e])都有公共點?若存在,求出最小的實數m和最大的實數M;若不存在,說明理由.
,e])都有公共點?若存在,求出最小的實數m和最大的實數M;若不存在,說明理由.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
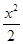 +
+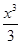 -
-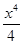 +…+
+…+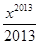 ,則下列結論正確的是( )
,則下列結論正確的是( )| A.f(x)在(0,1)上恰有一個零點 |
| B.f(x)在(0,1)上恰有兩個零點 |
| C.f(x)在(-1,0)上恰有一個零點 |
| D.f(x)在(-1,0)上恰有兩個零點 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com