
(本小題滿分12分)
向量
(1)若a為任意實數,求g(x)的最小正周期;
(2)若g(x)在[o, )上的最大值與最小值之和為7,求a的值,
)上的最大值與最小值之和為7,求a的值,
 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數學 來源: 題型:解答題
已知向量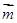 =(sinB,1-cosB),且與向量
=(sinB,1-cosB),且與向量 =(2,0)所成角為
=(2,0)所成角為 ,其中A、B、C是△ABC的內角。
,其中A、B、C是△ABC的內角。
(1)求角B的大小;
(2)求sinA+sinC的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
A﹑B﹑C是直線 上的三點,向量
上的三點,向量 ﹑
﹑ ﹑
﹑ 滿足:
滿足: -[y+2
-[y+2 ]·
]· +ln(x+1)·
+ln(x+1)· =
= ;
;
(Ⅰ)求函數y=f(x)的表達式;
(Ⅱ)若x>0, 證明f(x)> ;
;
(Ⅲ)當 時,x
時,x
 及b
及b
 都恒成立,求實數m的取值范圍。
都恒成立,求實數m的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com