
(本題14分)
△ABC中,角A、B、C的對邊依次為![]() 、
、![]() 、
、![]() .已知
.已知![]() ,
,![]() ,外接圓半徑
,外接圓半徑![]() ,
,
![]() 邊長為整數,
邊長為整數,
(1)求∠A的大小(用反三角函數表示);
(2)求邊長![]() ;
;
(3)在AB、AC上分別有點D、E,線段DE將△ABC分成面積相等的兩部分,求線段DE長的最小值.
 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:高中數學 來源: 題型:
(本題14分)如圖,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中點.
 (1)FD∥平面ABC;
(1)FD∥平面ABC;
(2)AF⊥平面EDB.
查看答案和解析>>
科目:高中數學 來源: 題型:
()(本題14分)如圖,矩形ABCD和梯形BEFC所在平面互相垂直,
,∠BCF=∠CEF=90°,AD=![]()
(Ⅰ)求證:AE∥平面DCF;
(Ⅱ)當AB的長為何值時,二面角A-EF-C的大小為60°?
查看答案和解析>>
科目:高中數學 來源:2011-2012學年甘肅省高三上學期期中考試理科數學試卷 題型:解答題
(本題14分)已知函數f (x) = ax3 +x2 -ax,其中a,x∈R.
(Ⅰ)若函數f (x) 在區間(1,2)上不是單調函數,試求a的取值范圍;
(Ⅱ)直接寫出(不需給出運算過程)函數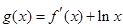 的單調遞減區間;
的單調遞減區間;
(Ⅲ)如果存在a∈(-∞,-1],使得函數 ,
x∈[-1, b](b > -1),在x = -1處取得最小值,試求b的最大值.
,
x∈[-1, b](b > -1),在x = -1處取得最小值,試求b的最大值.
查看答案和解析>>
科目:高中數學 來源:2010年廣東省高二上學期期中考試數學文卷 題型:解答題
.(本題14分)已知空間三點A(0,2,3),B(-2,1,6),C(1,-1,5)
⑴求以向量 為一組鄰邊的平行四邊形的面積S;
為一組鄰邊的平行四邊形的面積S;
⑵若向量 分別與向量
分別與向量 垂直,且
垂直,且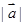 =
= ,求向量
,求向量 的坐標。
的坐標。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com