
如圖,△ 中,
中, ,
, ,
, ,在三角形內挖去一個半圓(圓心
,在三角形內挖去一個半圓(圓心 在邊
在邊 上,半圓與
上,半圓與 、
、 分別相切于點
分別相切于點 、
、 ,與
,與 交于點
交于點 ),將△
),將△ 繞直線
繞直線 旋轉一周得到一個旋轉體.
旋轉一周得到一個旋轉體.
(1)求該幾何體中間一個空心球的表面積的大小;
(2)求圖中陰影部分繞直線 旋轉一周所得旋轉體的體積.
旋轉一周所得旋轉體的體積.
科目:高中數學 來源: 題型:解答題
如圖,正方形ADEF與梯形ABCD所在平面互相垂直,AD⊥CD,AB//CD,AB=AD= ,點M在線段EC上且不與E、C垂合.
,點M在線段EC上且不與E、C垂合.
(1)當點M是EC中點時,求證:BM//平面ADEF;
(2)當平面BDM與平面ABF所成銳二面角的余弦值為 時,求三棱錐M—BDE的體積
時,求三棱錐M—BDE的體積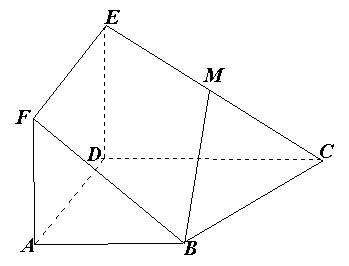
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,已知四棱錐P﹣ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC=3,側面PBC⊥底面ABCD,O是BC的中點.
(1)求證:DC∥平面PAB;
(2)求四棱錐P﹣ABCD的體積.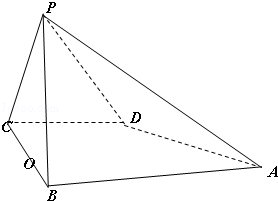
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(2013•湖北)如圖,某地質隊自水平地面A,B,C三處垂直向地下鉆探,自A點向下鉆到A1處發現礦藏,再繼續下鉆到A2處后下面已無礦,從而得到在A處正下方的礦層厚度為A1A2=d1.同樣可得在B,C處正下方的礦層厚度分別為B1B2=d2,C1C2=d3,且d1<d2<d3.過AB,AC的中點M,N且與直線AA2平行的平面截多面體A1B1C1﹣A2B2C2所得的截面DEFG為該多面體的一個中截面,其面積記為S中.
(1)證明:中截面DEFG是梯形;
(2)在△ABC中,記BC=a,BC邊上的高為h,面積為S.在估測三角形ABC區域內正下方的礦藏儲量(即多面體A1B1C1﹣A2B2C2的體積V)時,可用近似公式V估=S中﹣h來估算.已知V= (d1+d2+d3)S,試判斷V估與V的大小關系,并加以證明.
(d1+d2+d3)S,試判斷V估與V的大小關系,并加以證明.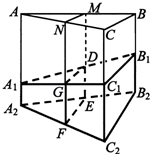
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,四棱錐F-ABCD的底面ABCD是菱形,其對角線 AE、CF都與平面ABCD垂直,AE=1,CF=2.
AE、CF都與平面ABCD垂直,AE=1,CF=2.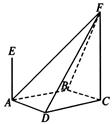
(1)求二面角B-AF-D的大小;
(2)求四棱錐E-ABCD與四棱錐F-ABCD公共部分的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知矩形 是圓柱體的軸截面,
是圓柱體的軸截面, 分別是下底面圓和上底面圓的圓心,母線長與底面圓的直徑長之比為
分別是下底面圓和上底面圓的圓心,母線長與底面圓的直徑長之比為 ,且該圓柱體的體積為
,且該圓柱體的體積為 ,如圖所示.
,如圖所示.
(1)求圓柱體的側面積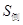 的值;
的值;
(2)若 是半圓弧
是半圓弧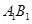 的中點,點
的中點,點 在半徑
在半徑 上,且
上,且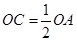 ,異面直線
,異面直線 與
與 所成的角為
所成的角為 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在△ABC中,∠ABC=90°,∠A=30。,斜邊AC上的中線BD=2,現沿BD將△BCD折起成三棱錐C-ABD,已知G是線段BD的中點,E,F分別是CG,AG的中點.
(1)求證:EF//平面ABC;
(2)三棱錐C—ABD中,若棱AC= ,求三棱錐A一BCD的體積.
,求三棱錐A一BCD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在三棱柱ABC-A1B1C1中,側棱AA1⊥底面ABC,AB⊥BC,D為AC的中點,AA1=AB=2,BC=3.
(1)求證:AB1∥平面BC1D;
(2)求四棱錐B-AA1C1D的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com